Hello, 👋🏻
Merci à tous d’être encore là pour cette 4ème édition.
La prochaine édition devra attendre fin août pour cause de vacances !
Et oui, il faut bien se reposer un peu. 😇 Mais pour me faire pardonner, je vous laisse choisir le sujet de la prochaine édition, en répondant au sondage, à la fin de cette page.
Et j’ai un code promo rien que pour vous ! Il est plus bas 👇🏻
La moyenne, cette cachottière.
Dans la dernière édition de “La Pause Maths”, je vous ai parlé des indicateurs de position, dont la moyenne.
Elle nous donne une idée globale des données, mais pour aller un peu plus loin, il nous faut d’autres types d’indicateurs.
👦🏻 Retrouvons Léo :
Lui et sa jumelle Sophia montrent leur bulletin de notes à leurs parents.
“Bravo les enfants, vous avez tout les deux eu 14 de moyenne en maths !”
Léo a un grand sourire, alors que Sophia peste :
“Mouais, enfin, Léo ne fait pas toujours grand chose, moi, je travaille beaucoup plus !”
Ce que veut nous dire Sophia, c’est qu’elle travaille pour avoir toujours de bonnes notes, alors que Léo se relâche et peut avoir de mauvaises notes. Mais elles sont compensées par ses très bonnes notes (quand il décide de travailler).
Hélas, ça, la moyenne nous ne le dit pas. 🤫 Quelle cachotière !
Nous avons alors besoins des indicateurs de dispersion !
Indicateurs de dispersion
Ils lèvent un peu le voile sur ce que nous cachent les indicateurs de position. Attardons-nous sur 4 indicateurs.
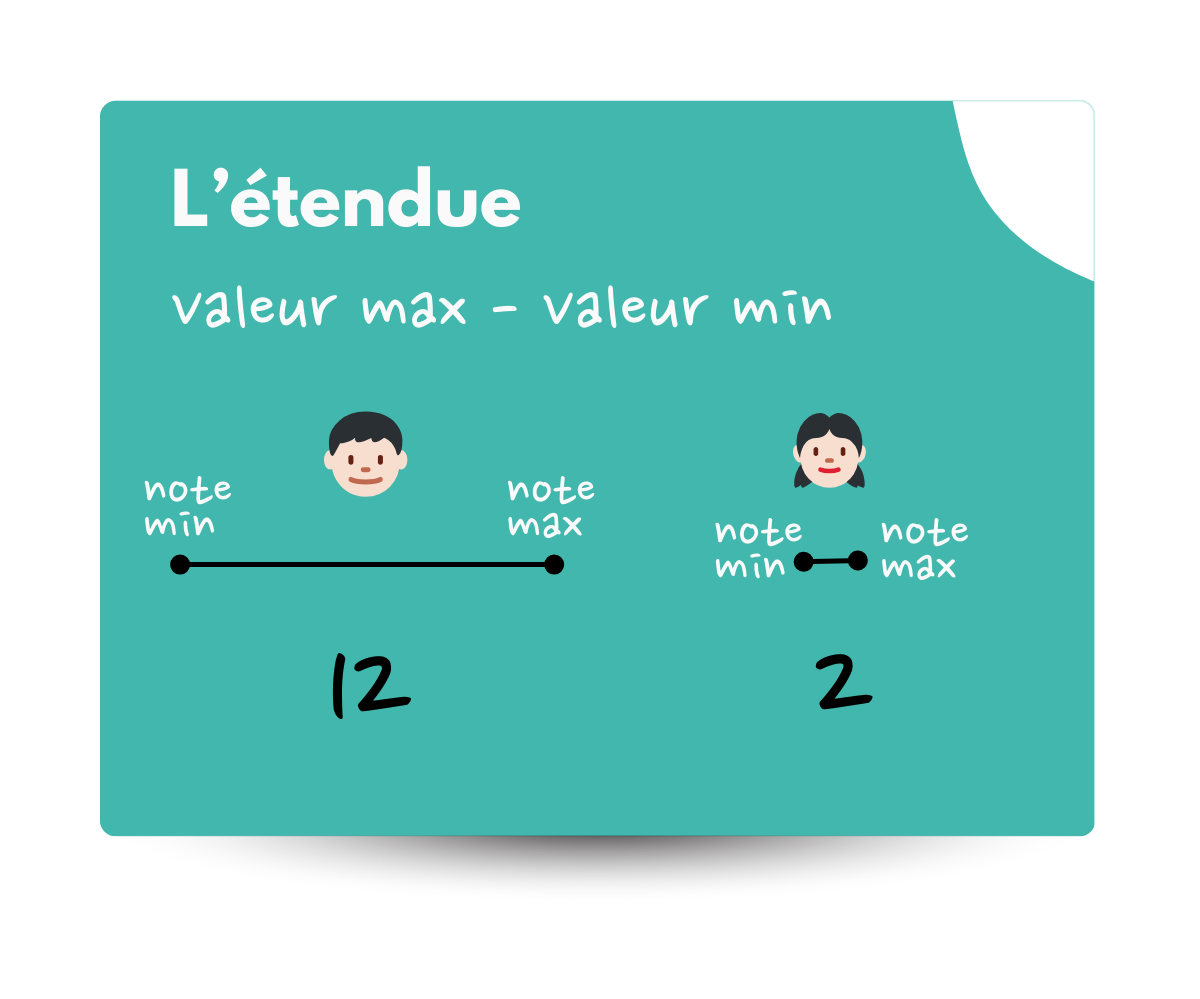
L’étendue.
Elle est très simple à calculer :
Il suffit de faire la différence entre la plus haute valeur et la plus basse.
Nous trouvons les étendues suivantes :
👦🏻 Léo : 12
👧🏻 Sophia : 2
Rien qu’avec cet indicateur, on comprend que Léo a des écarts de notes importants alors que Sophia a des notes toutes proches de 14.
Mais il se peut que Léo ait eu une seule mauvaise note. On ne peut pas lui coller une étiquette pour une mauvaise note.
L’étendue nous donne juste la plage sur laquelle sont réparties les notes.
Pour en savoir plus sur la dispersion des notes : regardons la variance.
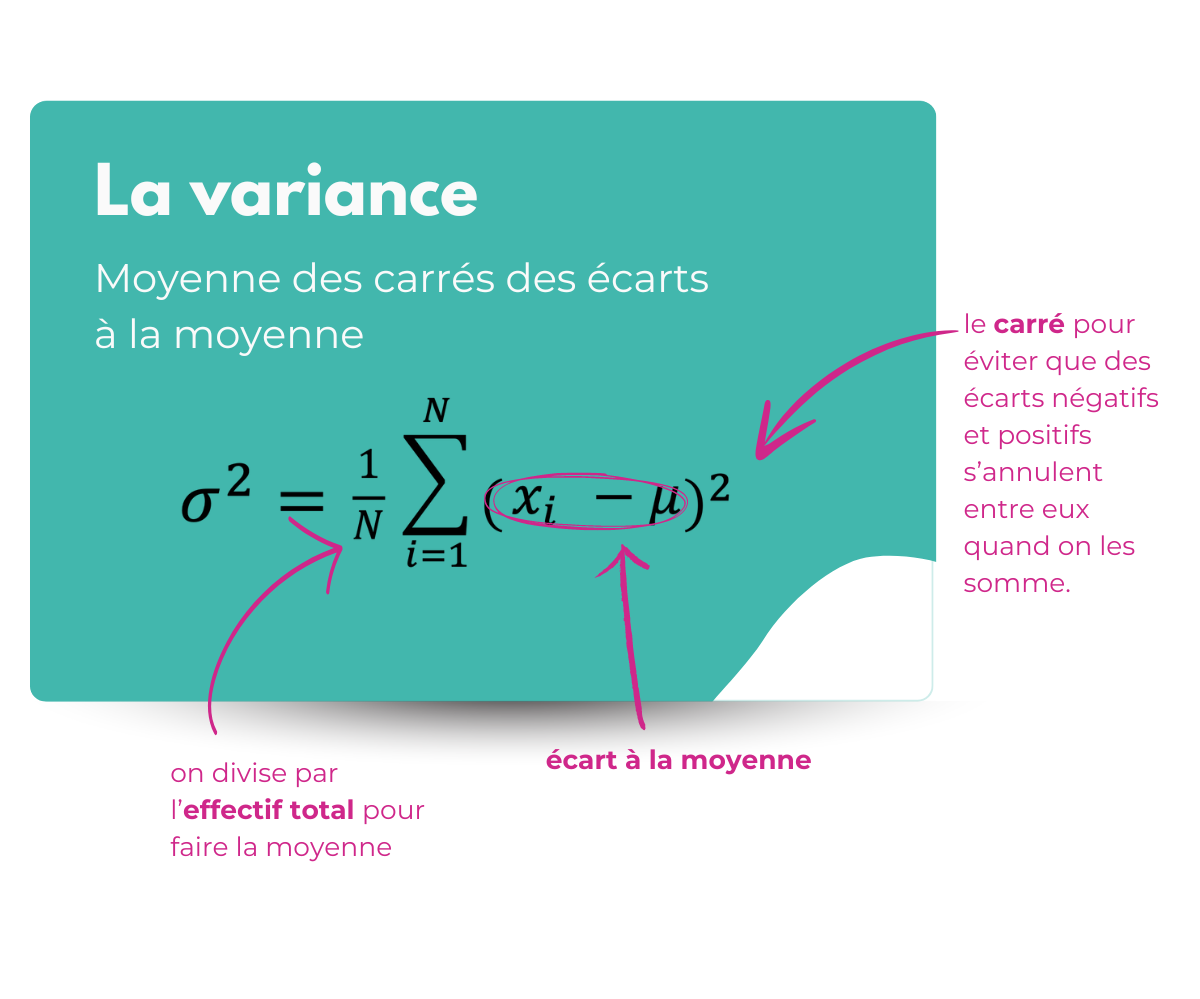
La variance
Comme son nom l’indique elle permet de mesurer à quel point les données varient. Et plus précisément l’écart entre les données et la moyenne.
Elle nous donne une idée de comment sont dispersées les données autour de la moyenne.
Seule, elle n’est pas évidente à interpréter mais elle nous permet de comparer deux jeux de données. Ici, on a les variances :
👦🏻 Léo : 25,7
👧🏻 Sophia : 0,7
Léo a une variance bien plus élevée. Ses notes sont plus dispersées autour de sa moyenne. Alors que Sophia, avec sa faible variance, montre qu’elle est régulière dans ses notes.
Le soucis avec la variance, c’est le carré !
Il est utile pour éviter que des écarts négatifs et positifs s’annulent entre eux, mais il change l’unité.
Si on a des données en mètre, la variance sera en mètre carré.
On va donc souvent se pencher sur un autre indicateur : l’écart-type qui est la racine carrée de la variance.
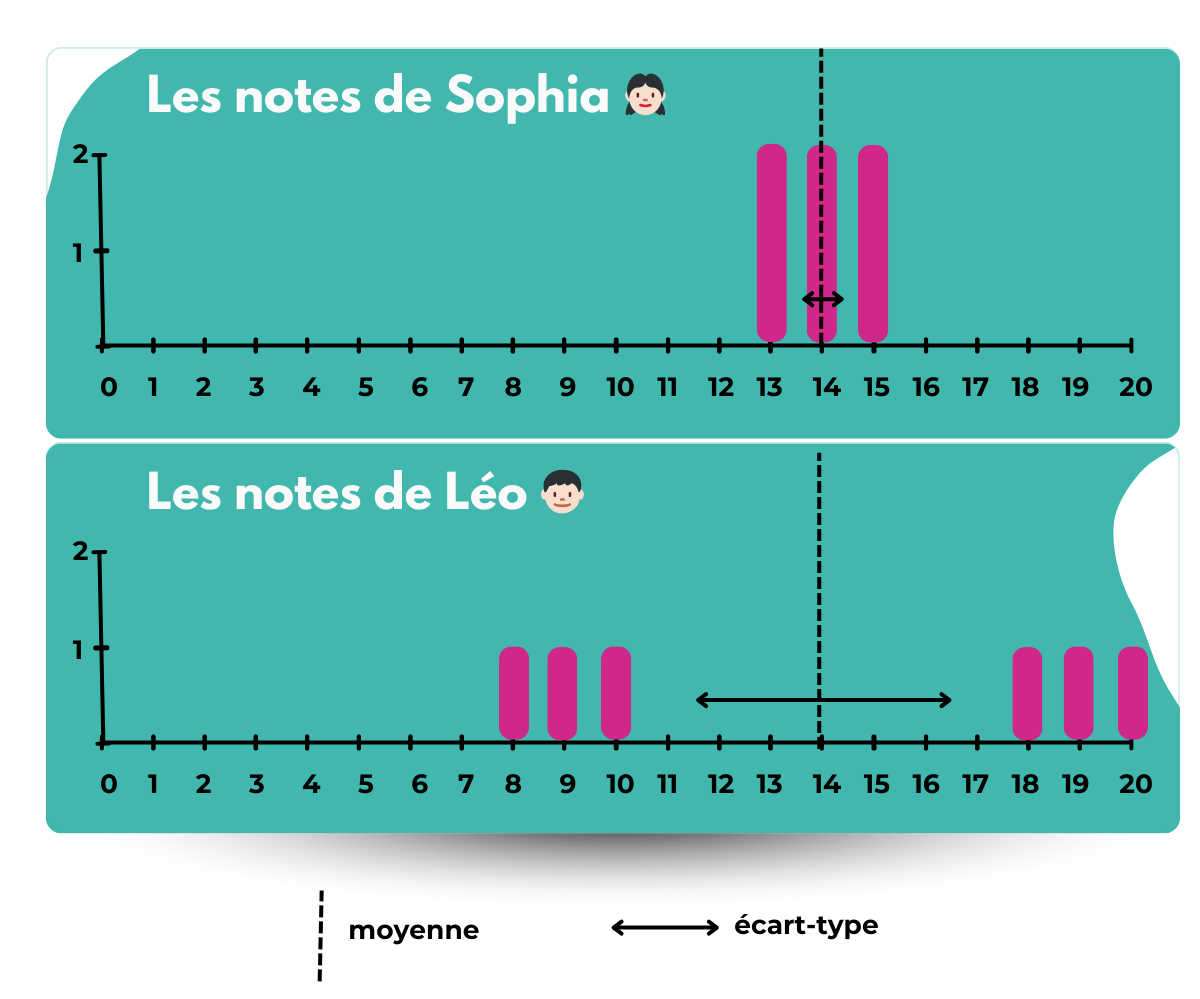
L’écart-type
Cet indicateur est dans la même unité que les données, et est donc plus facilement interprétable. Il sera souvent noté sigma (minuscule). La variance est parfois notée sigma au carré puisqu’elle est le carré de l’écart-type (comme sur l’image plus haut).
L’écart-type n’est pas seulement un indicateur, c’est aussi un outil.
Il permet, par exemple, de standardiser des données. On y reviendra dans une autre édition, mais en attendant, voici mon post Linkedin sur ce sujet : post
Vous avez donc compris que l'écart-type, comme la variance, indiquent comment les données sont dispersées autour de la moyenne.
Si la moyenne est une mesure centrale pertinente, ces deux indicateurs vont nous fournir des compléments d’information intéressants.
Dans notre exemple, ils nous permettent de mieux comprendre les profils de Léo et Sophia.
👦🏻 Les notes de Léo varient et sont dispersées autour de la moyenne. Elles ne sont pas stables.
👧🏻 Alors que Sophia est une élève qui fait preuve de régularité.
Mais il peut arriver que la moyenne ne soit pas la mesure centrale la plus pertinente. Parfois, la médiane est plus intéressante.
Dans ce cas : quel indicateur de dispersion regarder ?
Avant de répondre à cette question : petite pause blabla !
Je voulais vous remercier de vous être abonnés et de lire mes newsletters. Ça me prend beaucoup de temps, mais vos retours me font chaud au coeur.
J’ai donc créé un code promo pour Parcours Maths, spécialement pour vous 🤫, il vous permet de suivre ce parcours de mise à niveau à 180€ au lieu de 280€ ! 🎁
Il est valable cette semaine, donc jusqu’au dimanche 4 août minuit.
Le code : 180MERCI
Parcours Maths : c’est par ici.
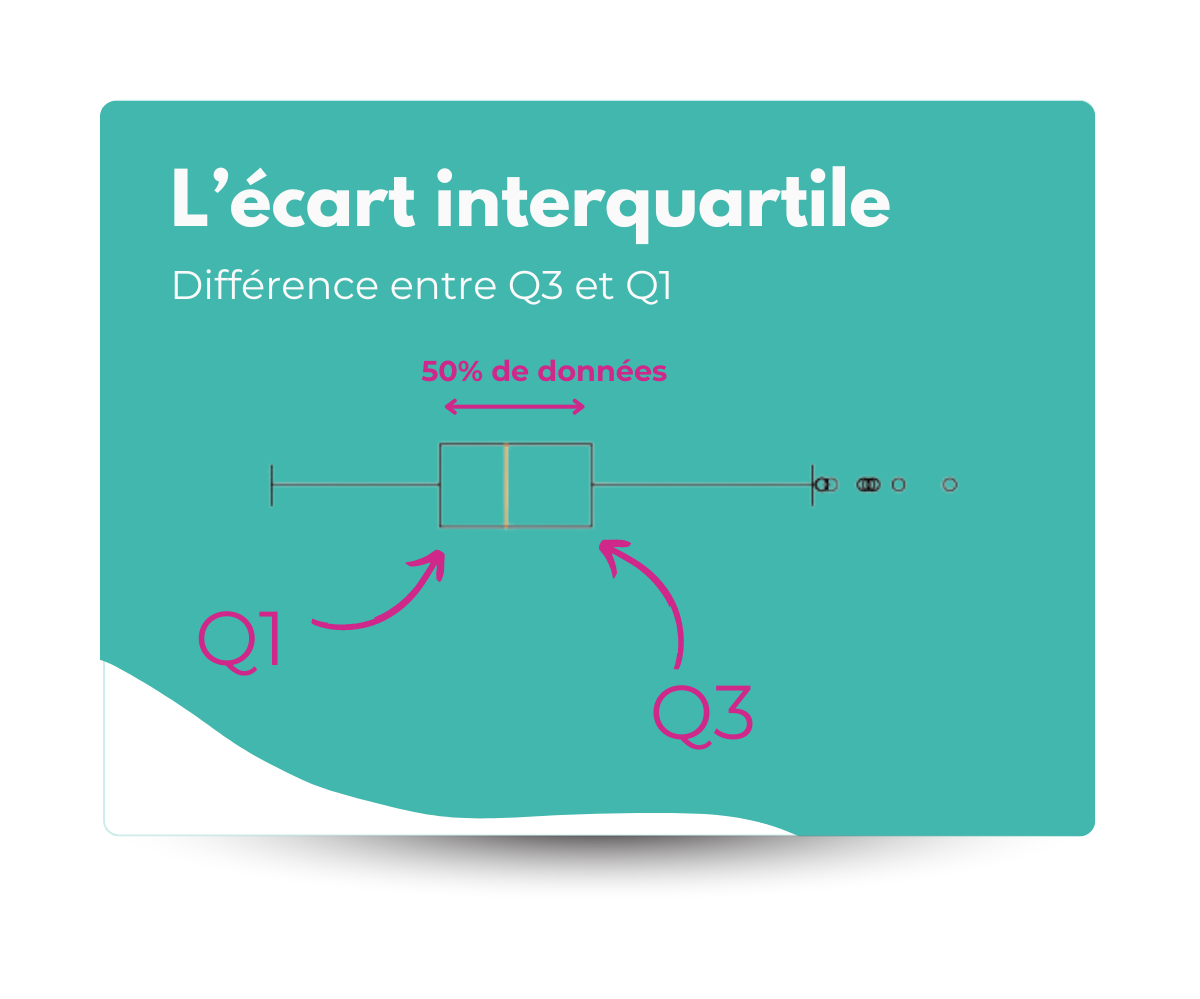
L’écart interquartile :
L’écart interquartile, comme l’étendue, est une simple différence. C’est la différence entre le 3ème quartile et le 1er quartile.
Q3 - Q1
On retrouve cet écart sur les boxplots (ou boîte à moustache).
Cet indicateur se concentre sur la dispersion des 50% des données situées au centre. Comme la médiane, il n’est pas sensible aux valeurs extrêmes ou aux outliers.
Il est très utile dans le cas où les données ne sont pas symétriques. Et oui, vous pouvez être confrontés à des distributions asymétriques.
Dans ce cas, la moyenne, impactée par les grandes valeurs, n’est pas forcément l’indicateur central le plus pertinent. La médiane peut être plus intéressante.
Et de la même manière, la variance ou l’écart-type seront impactés par ces grandes valeurs. L’écart interquartile lui, ne se laisse pas berner par ces valeurs et nous donne une bonne indication sur la dispersion des données centrales.
Attention : il faut toujours prendre en compte le contexte et ce que l’on cherche pour choisir un indicateur. Parfois, malgré une distribution asymétrique, la moyenne sera l’indicateur le plus pertinent.
Aller, on conclue avec ce résumé 😉
Indicateurs de position VS indicateurs de dispersion
Les indicateurs de position, parfois appelés mesures de tendance centrale, décrivent la localisation centrale des valeurs d'un ensemble de données. Ils indiquent où se situent la plupart des données. .
Par exemple, comme dit plus haut, la moyenne est utile pour des données symétriques, tandis que la médiane est préférée pour des distributions asymétriques.
Les indicateurs de dispersion, ou mesures de variabilité, décrivent l'étendue ou la dispersion des valeurs dans un ensemble de données. Ils indiquent dans quelle mesure les valeurs diffèrent les unes des autres et de l'indicateur de position.
Par exemple, une faible variance indique que les valeurs sont proches de la moyenne, tandis qu'un grand écart interquartile signale une large dispersion des valeurs centrales.
Utiliser ces deux types d’indicateurs nous donne une meilleure perception des données ! 😉
En attendant la prochaine édition, je vous souhaite de bonnes vacances 🌞, enfin, pour ceux qui en prennent, courage pour les autres 💪🏻
Et je vous laisse choisir le sujet pour la prochaine fois :
À bientôt ! 👋🏻
Anne-Lise.