Bonjour tout le monde ! 👋🏻
Cette 6ème édition fait suite à la dernière. On continue sur la logique mathématique cette semaine, puis on passera à d’autres notions 😉
Sinon, pour ceux qui auraient loupé l’info : vous pouvez maintenant me retrouver sur Instagram ! 🙂 Je vous mets la toute 1ère vidéo Insta juste ici 👇🏻
Mais maintenant, continuons dans la logique !
Thalès et Pythagore nous avaient montré la voie !
Au-delà des histoires de triangles, Thalès et Pythagore nous apprennent quelque chose d’utile !
Au collège, quand on arrive aux théorèmes de ces deux mathématiciens, on se demande à quoi cela va nous servir ?
Alors, on apprend un peu “bêtement” par coeur et on les applique aux exercices donnés par le prof, puis on les oublie ! 🤷🏻♀️
Pourtant, à ce moment précis de notre scolarité, on découvre, sans y prêter trop attention, la notion de contraposée et de réciproque !
Comprendre ces 2 notions de logique pourrait bien nous éviter de dire des bêtises (que l’on dit parfois avec aplomb 😅 ).
Pour vous expliquer ce point, je ne vais pas parler de Pythagore mais du petit Léo (3 ans). 👦🏻
La réciproque
👩🏻 Sa maman sait une chose sur Léo (qui est vérifié à chaque fois, on peut considérer ça comme une vérité) :
Quand Léo doit manger des haricots, il se met à pleurer ! 😭
Aujourd’hui, la mère de Léo va le récupérer chez sa nourrice. Cette dernière explique que Léo n’a pas arrêté de pleurer pendant le repas.
❓Sa maman peut-elle en conclure que Léo a mangé des haricots ?
Et bien non !! ❌
Même si c’est probable, on ne peut pas l’affirmer.
Regardons la situation d’un point de vue logique.
On note :
A = Léo doit manger des haricots
B = Léo pleure
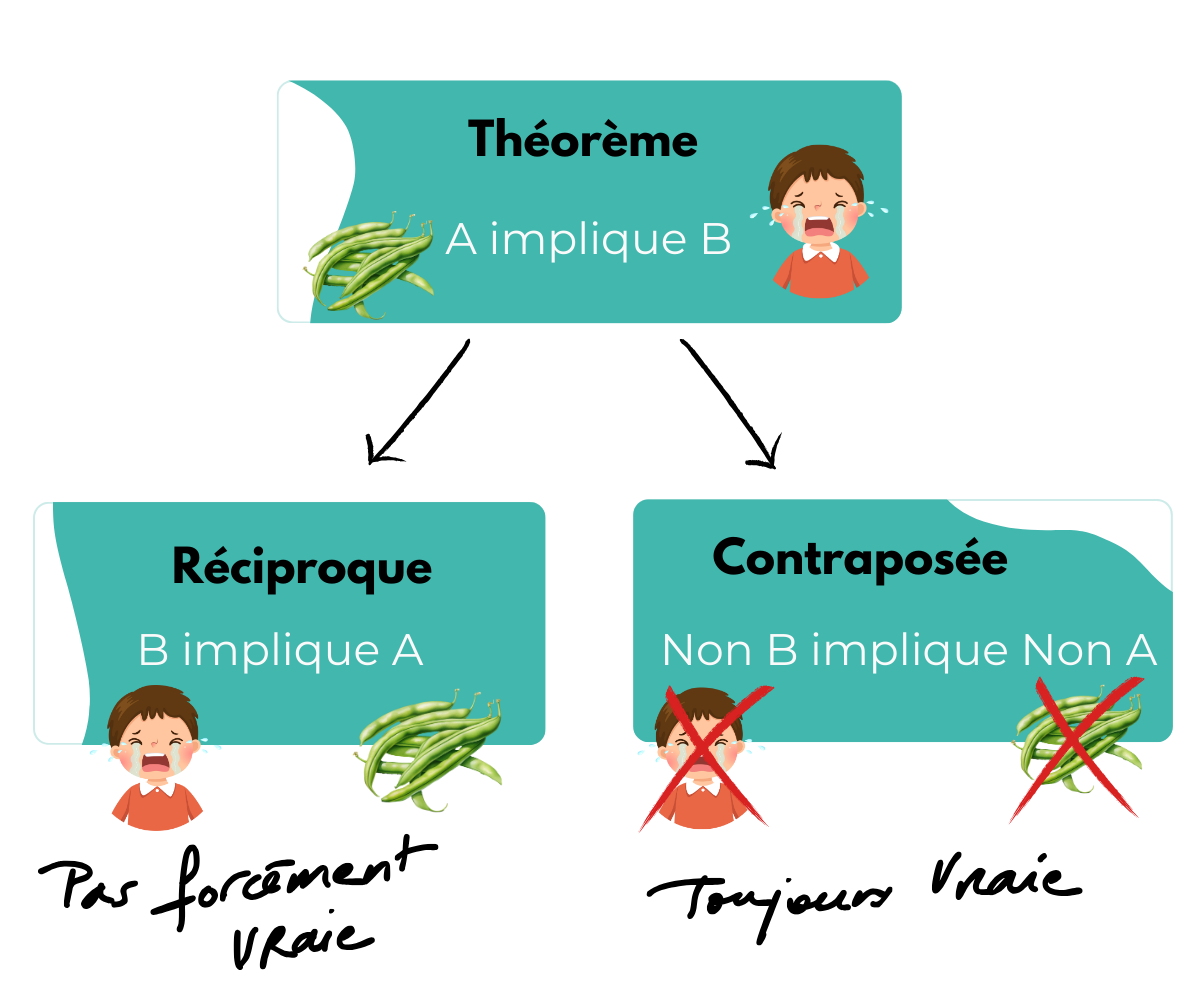
Nous savons que A implique B. ☝🏻Appelons ça le théorème des haricots.
La réciproque du théorème des haricots est : B implique A.
Autrement dit : Si Léo pleure alors il doit manger des haricots.
Mais une réciproque n’est pas forcément vraie !
Et oui, il n’y a pas que les haricots qui font pleurer Léo. Vous pensez vraiment qu’il serait ravi devant des épinards ? 😅
Le fait que A implique B ne veut pas dire que B implique A.
Et je vous assure que j’entends souvent cette erreur.
Parfois, elle est un peu plus délicate à déceler.
La contraposée.
La contraposée a de quoi se vanter devant la réciproque.
Parce qu’elle, elle est toujours vraie !
Contraposée : Si A implique B alors non B implique non A
Avec le théorème des haricots cela donne :
Si Léo ne pleure pas alors il ne doit pas manger des haricots.
Si la nourrice dit à la maman “tout s’est bien passé, il n’a pas pleuré lors du repas”, sa mère peut être certaine que les haricots n’étaient pas au menu !
Le contre-exemple
Regardons maintenant du côté du contre-exemple.
Si je vous dis que tous les chats sont roux, comment pouvez-vous me montrer que j’ai tort ?
Tout simplement en me montrant un chat qui n’est pas roux.
En logique mathématique, c’est ce qu’on appelle un contre-exemple. Il permet de montrer facilement que quelque chose est faux.
Mais cela ne marche pas dans l’autre sens. Un exemple ne suffit pas à montrer que quelque chose est vrai. Pour vous prouver que tous les chats sont roux, il faudrait que je vous montre tous les chats de l’univers !
Ici, l’exception ne confirme absolument pas la règle 😅
Dans la vie de tous les jours
Lors d’un repas avec des amis, nous parlions de la conservation des aliments, l’importance de mettre au frais, etc (ce genre de discussion qui confirme que l’on a dépassé les 30 ans 😂).
Vous avez déjà vu quelqu’un laisser son poulet décongelé dans le four toute une nuit, non ?
Peut-être même que vous le faites et là, je vous laisse aller voir les newsletters de The French Virologist sur le sujet !
On parlait donc du risque de contamination avec ces pratiques. Et là, quelqu’un sort le fameux “j’ai toujours fait ça et je ne suis jamais tombé malade” !
Aller, entre-nous, on a tous déjà dit quelque chose dans le genre. 😇
Ici, on utilise un exemple personnel pour essayer de montrer que l’autre a tort. Sauf que cet exemple ne prouve rien.
En logique, un contre-exemple valide peut réfuter une généralité. Par exemple, si quelqu’un affirmait que personne ne tombe malade en laissant décongeler de la viande à température ambiante, il suffirait d’une personne ayant été intoxiquée dans cette situation pour montrer que c’est faux. Ce serait alors un contre-exemple.
Mais dans notre cas, la situation est différente.
Logiquement, on pourrait dire :
A : Certaines personnes tombent malades après avoir laissé de la viande décongeler à température ambiante.
B : Il y a un risque d’intoxication en laissant la viande décongeler à température ambiante.
Le raisonnement est : A implique B.
La contraposée, qui est aussi vraie, est : Non B implique Non A.
Autrement dit, s'il n'y avait aucun risque, alors personne ne tomberait malade de cette manière.
Quand quelqu’un rétorque “je le fais, et je n’ai jamais été malade” pour contester l’existence d’un risque, il commet une erreur de raisonnement. Cette personne généralise son expérience personnelle à toutes les situations, sans preuve.
Ce n’est pas un contre-exemple, c’est un exemple isolé, qui ne suffit pas à prouver que le risque n’existe pas !
Pour réfuter l’affirmation “il y a un risque d’intoxication”, il faudrait prouver que personne n’a jamais été intoxiqué de cette manière, ce qui est impossible. ❌
Et ce genre de raisonnement est très courant !
On pourrait alors discuter des biais cognitifs qui nous font dévier de la logique pure, mais comme je le disais dans la dernière édition, nous ne sommes pas des robots 🤖 mais des humains remplis de nuances et de contradictions !
Toutefois, comprendre un peu plus la logique, ferait du bien à tout le monde 😉
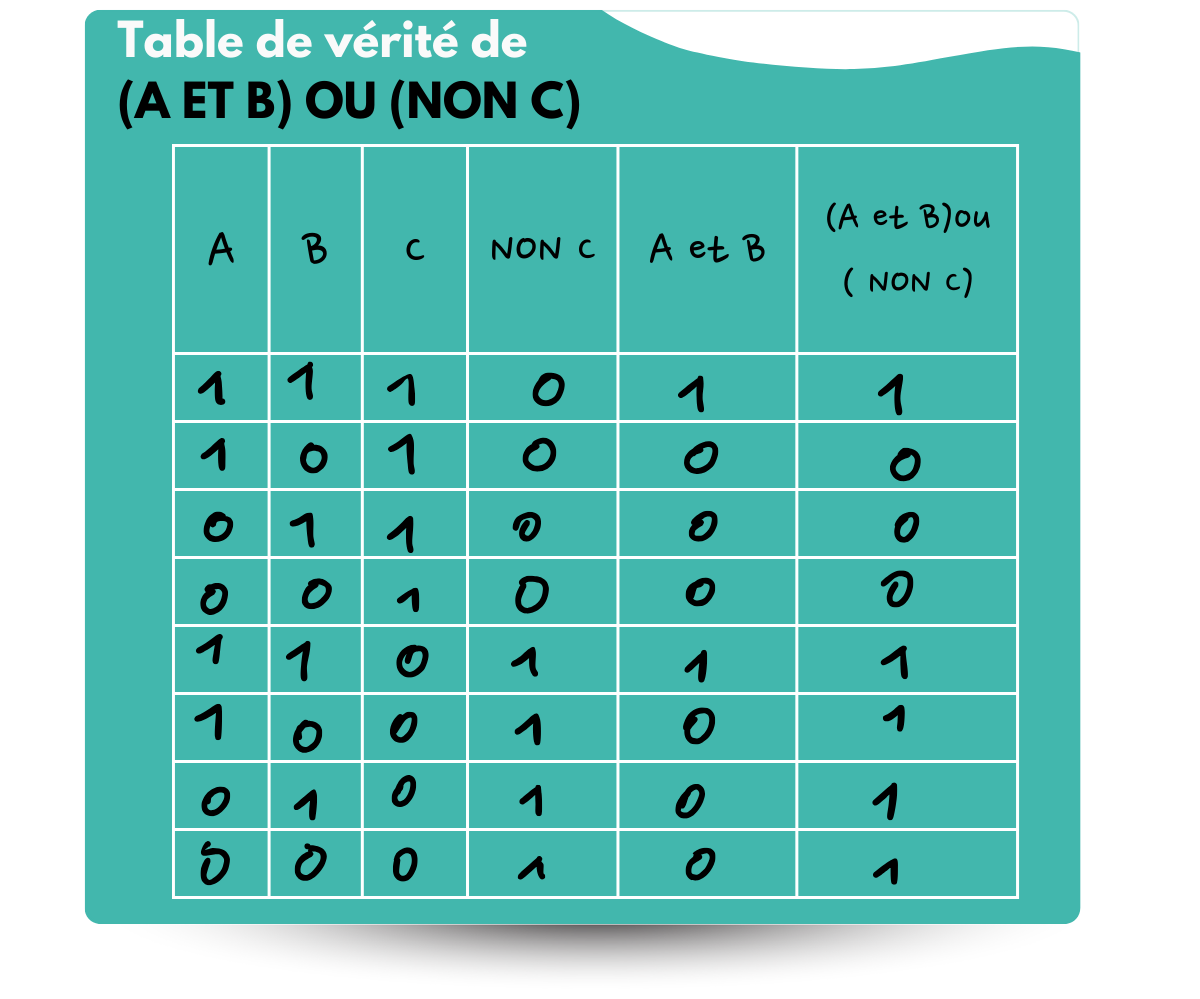
D’ailleurs en parlant de la dernière édition, je vous avais laissé avec un exercice, voici la correction :
On se retrouve dans deux semaines, pour aborder un autre sujet mathématique.
En attendant, rejoignez-moi sur Linkedin, Instagram ou encore Facebook !
À bientôt 👋🏻
Anne-Lise.