😱 Je n’ai pas fait de newsletter ces 2 derniers mois !!! 😱
Oups ! Désolé ! J’étais un peu beaucoup occupée…
Aujourd’hui, j’ai pris le temps de vous écrire parce que j’ai très envie de vous parler d’un projet sur lequel je bosse depuis des mois 😊
(Mais on va quand même faire des maths dans cette édition !)
👉🏻 L’histoire :
Pour entrer en formation de data scientist, une de mes élèves avait besoin de base en algèbre linéaire. Je n’avais rien de prêt, alors j’ai créé un cours..
J’en ai fait profiter d’autres élèves. Puis l’idée d’en faire un cours en autonomie a germée.
Comme à mon habitude, j’en parle sur LinkedIn et effectivement plusieurs personnes étaient intéressées.
Le soucis : entre l’idée et la réalisation, il s’est passé… des mois 😅
🌞 Mais cet été, je finis ce cours !!!
Vidéos de cours, fiches d’exercices, fiches de cours.
J’ai prévu tout un parcours pour vous guider, pas à pas, pour maîtriser les concepts fondamentaux de l’algèbre linéaire et enfin comprendre mathématiquement l’A.C.P.
📚 Au programme :
✔️ Les ensembles
✔️ Les structures algébriques
✔️ Les applications
✔️ Les espaces vectoriels
✔️ Les applications linéaires
✔️ La diagonalisation d’une matrice
✔️ L’Analyse en Composantes Principales📆 Le lancement est prévu pour la rentrée.
Et qui dit lancement, dit promo !! 🤩
Mais, j’aime proposer une meilleure offre à celles et ceux qui me disent
“intéressé(e) 🤚🏻”
avant le lancement… car c’est grâce à eux que je garde la motivation !
Déjà près de 50 personnes sur la liste V.I.P.
Tu veux en être ?
C’est par ici : https://maprofdemaths.systeme.io/algebre_lineaire
⚠️ Prérequis
Pour profiter pleinement de ce cours, il faut déjà avoir quelques bases (niveau lycée) : fonctions, vecteurs, matrices, déterminant, stats descriptives (variance, covariance…).
Je ferai quelques rappels, mais si tout ça te semble flou, une petite remise à niveau te sera utile avant de te lancer.
Et justement, aujourd’hui on parle de matrices (belle transition haha !)
Les matrices
Déjà, c’est quoi ?
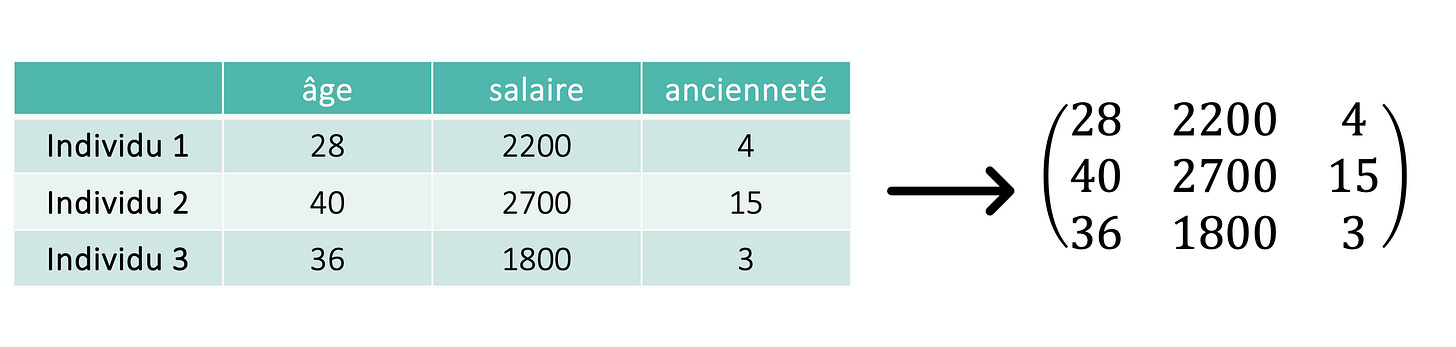
Une matrice, c’est simplement un tableau de nombres.
C’est un peu comme une feuille Excel : des lignes, des colonnes, et des valeurs.
Donc tu en as déjà vu.
👉🏻 La taille d’une matrice, c’est :
nombre de lignes × nombre de colonnesPar exemple, une matrice qui a 3 lignes et 4 colonnes, a pour taille : 3 x 4
👉🏻 Une matrice un objet mathématique.
Il y a plein d’objets mathématiques :
les nombres, les suites, les fonctions, les vecteurs, les matrices etc.
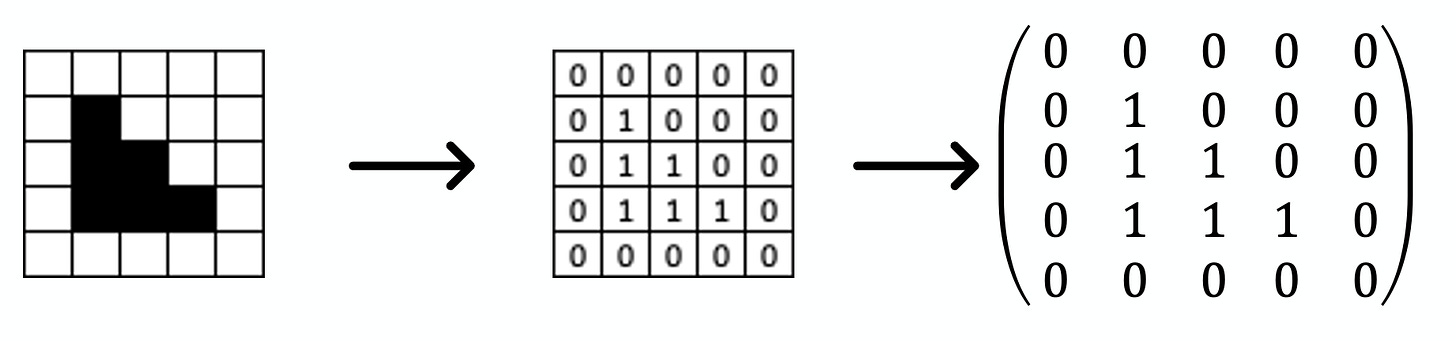
Ce que représente une matrice peut varier : une image, des données, une transformation géométrique…
Peu importe ce qu’elle signifie dans un contexte donné, les règles de calcul restent les mêmes.
Aujourd’hui, je te montre 2 calculs de base.
1️⃣ L’addition de matrices.
C’est l’opération la plus simple.
Si tu veux faire :
A + BIl faut que A et B aient exactement la même taille
✅ même nombre de lignes et même nombre de colonnes.
Le résultat est une matrice de la même taille, et chaque valeur est la somme des deux valeurs correspondantes dans A et B.
Facile, non ?
✏️ À toi d’essayer :
Réponse :
2️⃣ La multiplication de matrices
Là, c’est un peu plus subtil.
Pour faire :
A × B Il faut :
✅ nombre de colonnes de A = nombre de lignes de B.
Sinon, la multiplication n’est pas définie.
Ici :
A = matrice 3×2
B = matrice 2×3
✅ Les colonnes de A = 2 = les lignes de B → on peut faire la multiplication
💡 Taille du résultat :
(nombre de lignes de A) × (nombre de colonnes de B)Dans notre exemple, le résultat sera une matrice 3×3
👉🏻 Comment faire la multiplication ?
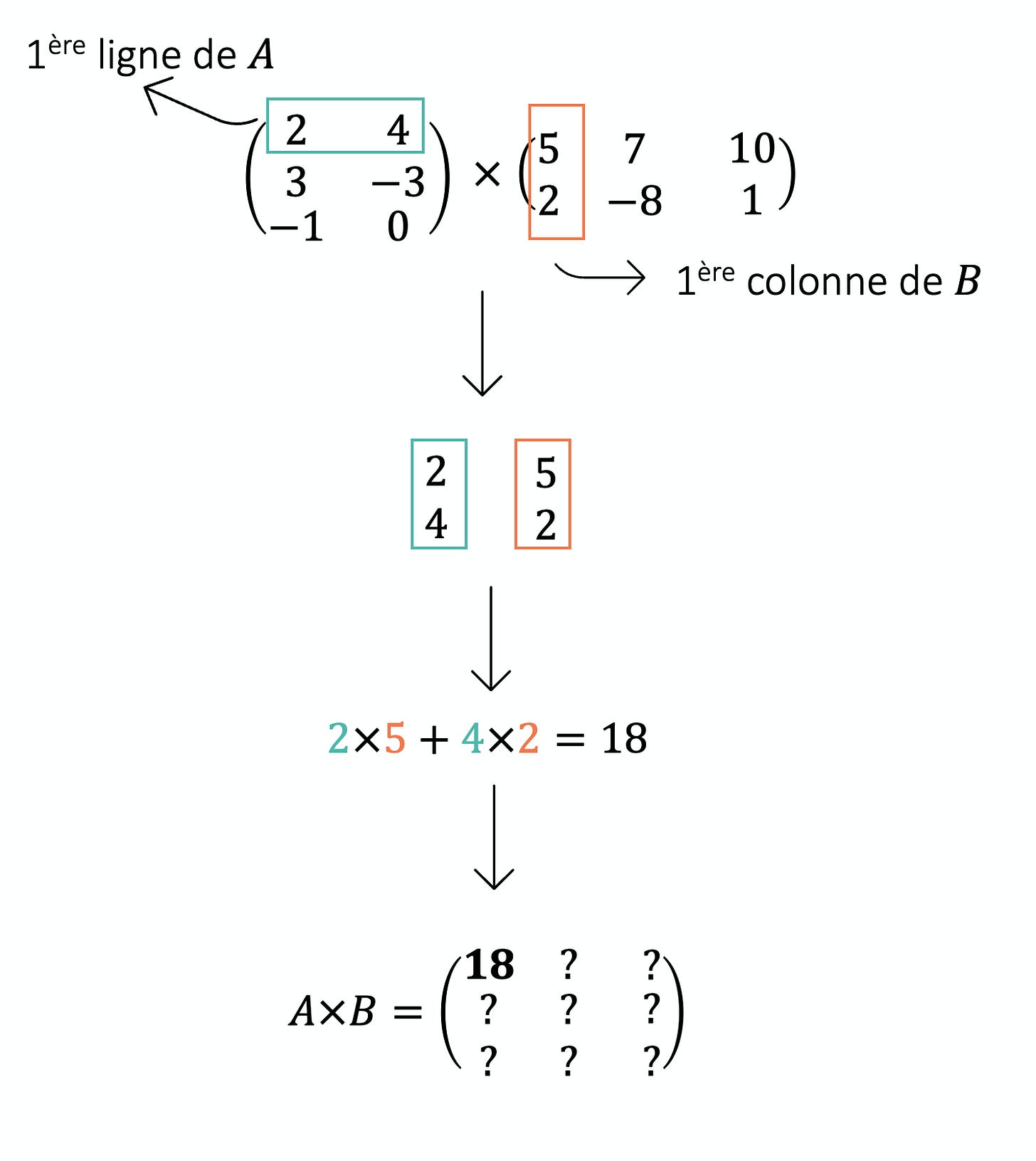
Pour calculer la valeur en 1ère ligne, 1ère colonne du résultat, on prend :
la 1ère ligne de A
la 1ère colonne de B
et on fait le produit scalaire (multiplication terme à terme + addition)
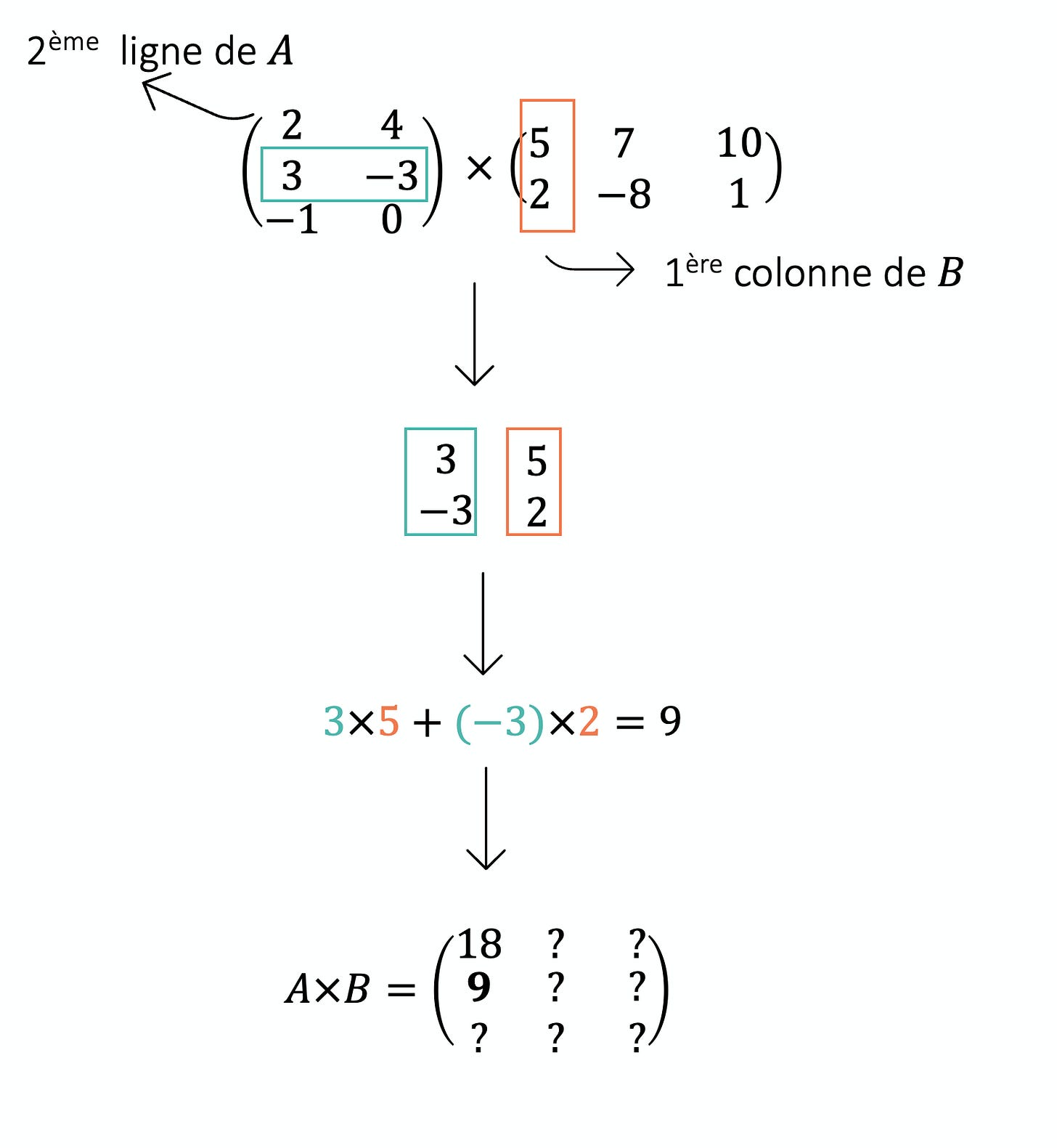
On répète ça pour chaque ligne de A et chaque colonne de B, ce qui nous donne une nouvelle matrice.
✏️ À toi de jouer : je te laisse avec deux matrices.
→ Est-ce que tu peux les additionner ? Les multiplier ?
→ Quelle est la taille du résultat ?
→ Fais le calcul 😇
(Réponses juste après 👇)
👇 réponses👇
→ A a pour taille 3x2 et B a pour taille 2x2
On ne peut pas les additionner car elles n’ont pas la même taille.
Par contre, on peut les multiplier puisque :
nombre colonnes de A = nombre lignes de B → Le résultat sera une colonne 3x2
C’est tout pour aujourd’hui !
Je retourne bosser sur le cours d’algèbre linéaire 😉
🤩 S’inscrire à la liste VIP 🤩
https://maprofdemaths.systeme.io/algebre_lineaire
Profitez bien de vos vacances et à bientôt pour faire chauffer vos méninges !
Anne-Lise.


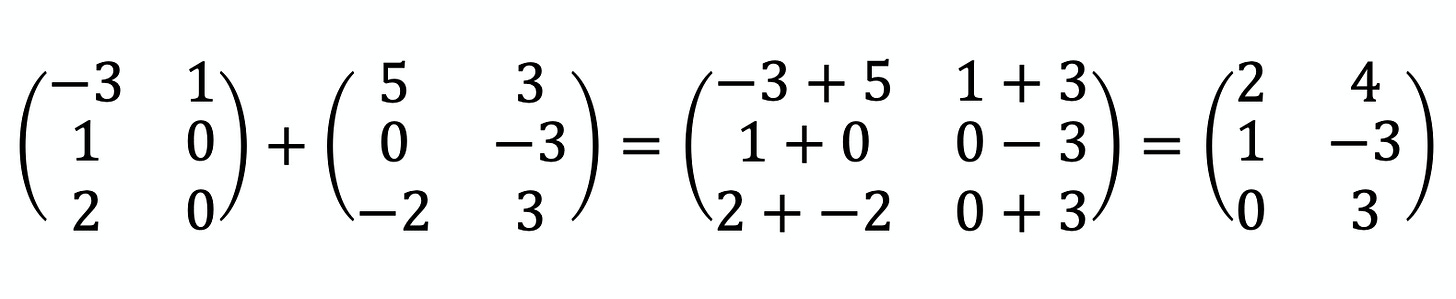
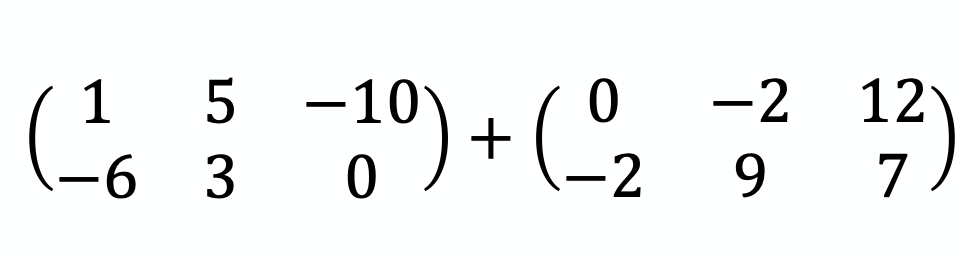

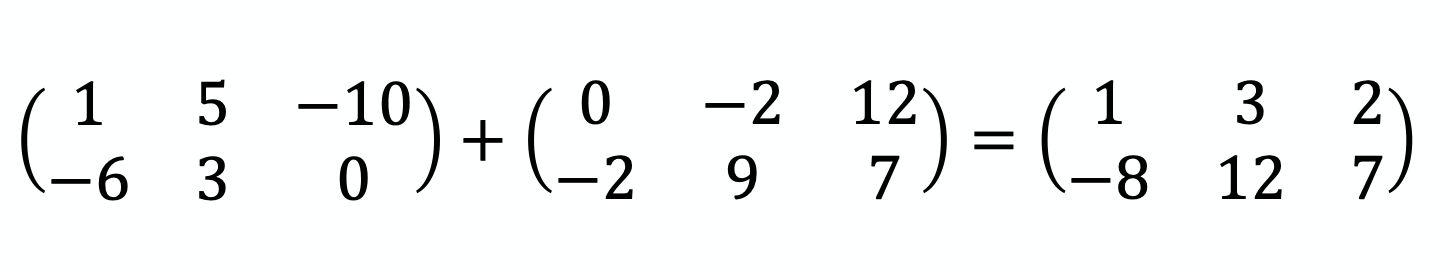
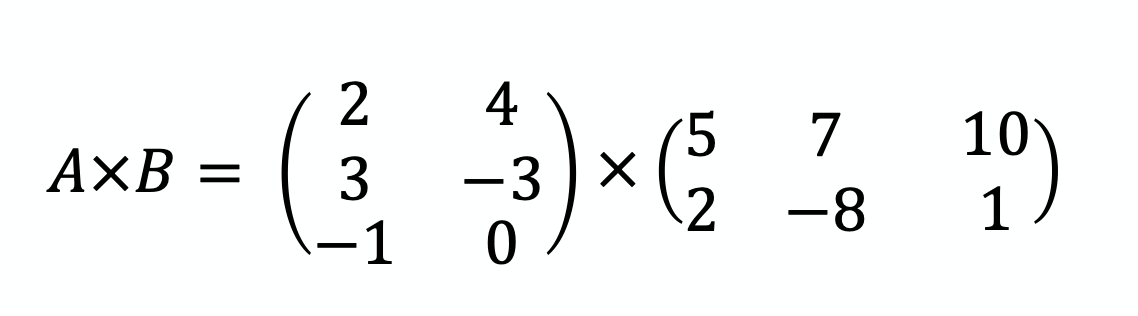
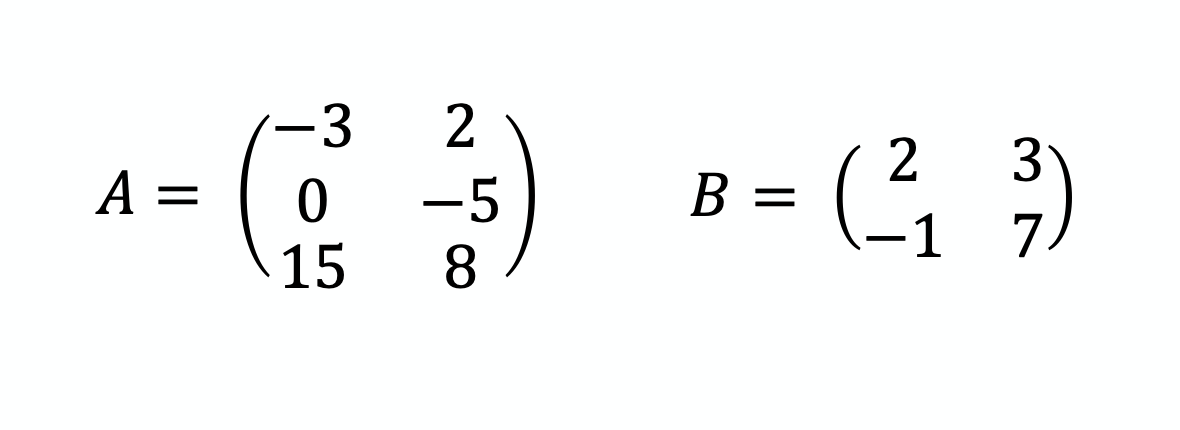

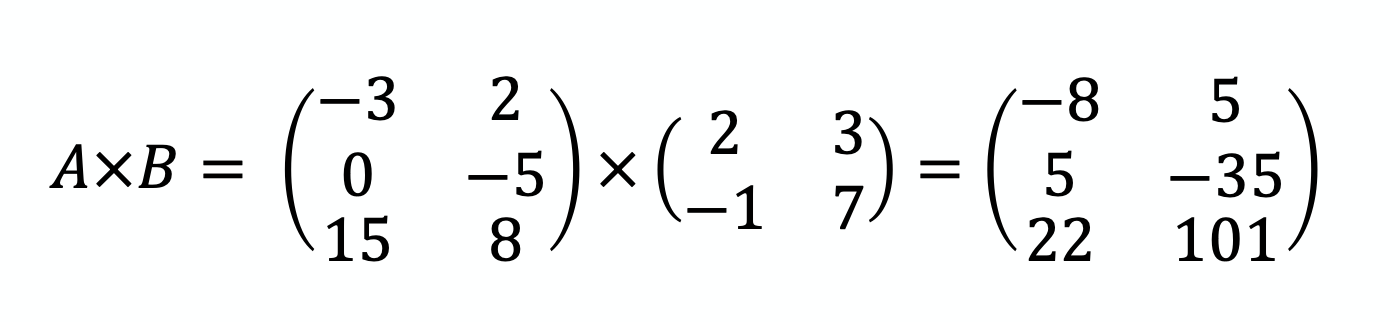
Quel retour tonitruant avec ces opérations matricielles, vieux souvenirs de plus de 50 ans en arrière 🤗. Merci Anne-Lise
Merci pour ces rappels ! J'aimerais pointer que "Il faut que A et B aient exactement la même taille
✅ nombre de lignes = nombre de colonnes" peut laisser penser que les matrices qu'on additionne doivent avoir un nombre de lignes égal à leur nombre de colonnes.