Bonjour à tous ! 👋🏻
L’importance des maths en data est souvent sous-estimée.
J’ai rencontré plusieurs personnes qui se sont lancées en data (analyse ou science) sans être passé par la case maths. Alors, elles apprennent à écrire la ligne de code pour faire tel ou tel ou modèle. Mais, elles sont perdues devant les formules.
Dans ces circonstances, une simple régression linéaire reste mystérieuse.
Avec mes élèves, quand on arrive à la fonction affine, les premières étincelles apparaissent.
”Ahhhh ! Mais je comprends mieux la régression linéaire maintenant !”
La fonction affine, on la découvre en classe de seconde.
Revoir les bases en maths niveau lycée, c’est déjà une étape importante. Cela va vous éclairer sur beaucoup de modèles que vous apprendrez lors de votre formation en data.
Dans cette édition, on va se pencher sur la fonction affine.
Les fonctions
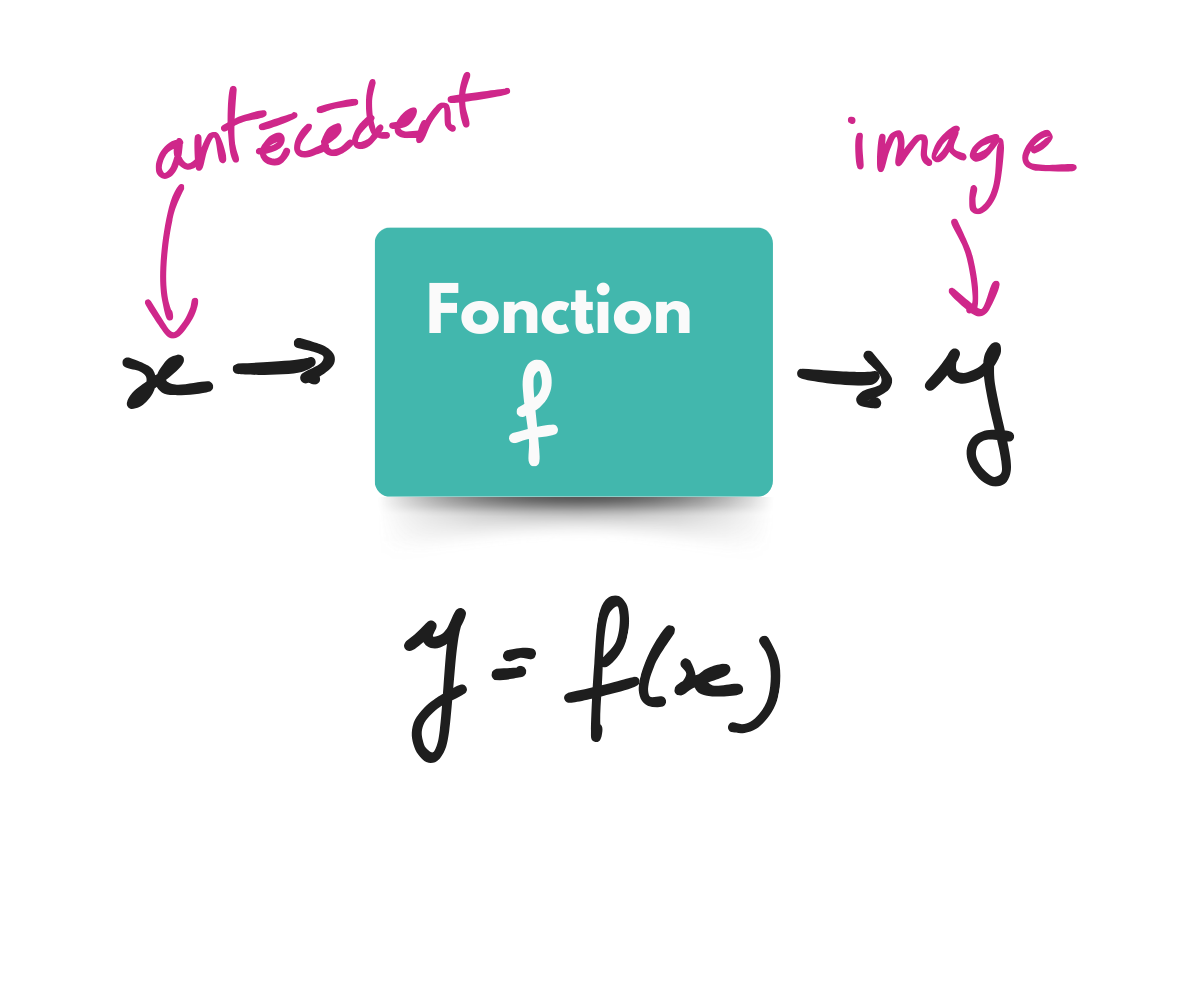
De manière générale, on peut voir une fonction comme une machine.
On lui donne une valeur (x qu’on peut appeler “variable” car c’est une valeur qui peut varier) et la fonction nous donne une autre valeur (qu’on appelle image, ici, notée y). Cette nouvelle valeur vient d’un calcul fait à partir de la valeur qu’on lui a donnée.
Regardons d’un peu plus près ce qu’est une fonction affine.
Fonction affine
On peut appréhender cette fonction de deux manières :
algébriquement avec son équation : f(x) = ax+b
géométriquement avec sa représentation graphique. La fonction affine est représentée par une droite.
Prenons un exemple :
Une entreprise facture un abonnement de base de 25€ par mois, pour regarder 5 films en ligne par mois. Puis, s’ajoute à l’abonnement 5€ par films supplémentaires visionnés. Si vous avez vu 7 films (dont 2 films supplémentaires), combien allez-vous payer ?
Le calcul est :
25 + 2x5 = 35€
On peut aussi lire le résultat sur le graphique.
35 est l’image de 2 par la fonction affine f.
Et quelle est l’équation de cette fonction ?
f(x) = 5x + 25
👉🏻 De manière générale, pour une fonction affine on a : f(x) = ax + b
(avec a et b des réels).
Coefficient directeur.
a est le coefficient directeur de la droite.
C’est un élément très important à comprendre. Il est utile par la suite pour comprendre les dérivées, la régression linéaire etc.
Ce coefficient directeur, c’est en fait la pente de la droite. Il nous dit si la droite “monte” ou “descend” et à quel point la pente est importante.
Il nous dit aussi de combien va augmenter le résultat (l’image) si on ajoute 1 à la valeur d’entrée.
Exemple :
f(x) = 5x + 25
Le coefficient directeur est 5.
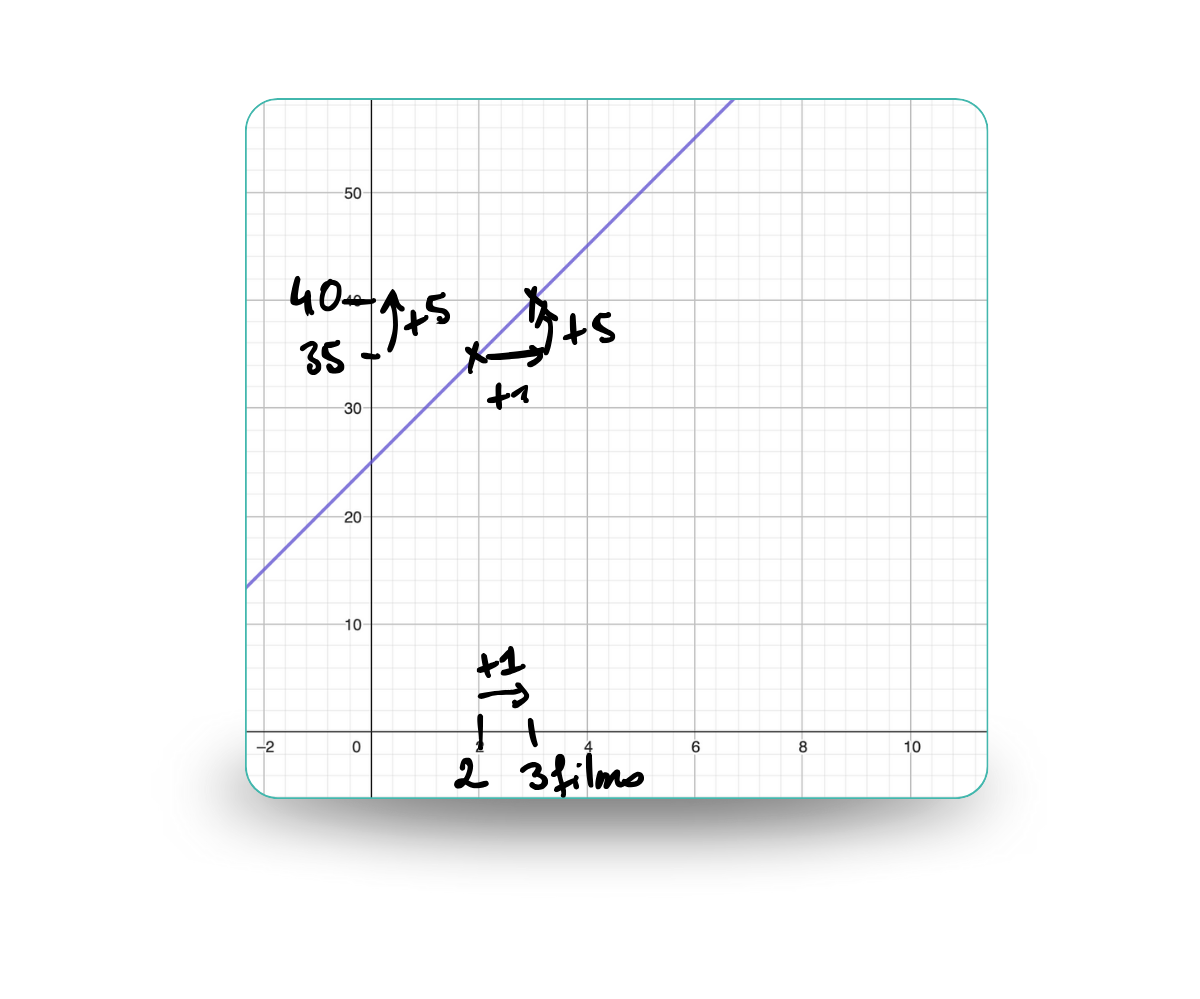
Cela veut dire que pour 1 pas sur l’axe des x (donc si on ajoute 1 à x) on monte de 5 pas sur l’axe des y (on aura +5 à l’image)
Ou dans notre situation, si on regarde 1 film supplémentaire, on paiera 5€ de plus.
En effet : f(2) = 5x2 + 25 = 35
f( 2 + 1) = f(3) = 5 x 3 + 25 = 40
On a bien f(2+1) = f(2) + 5
👉🏻 De manière générale :
f(x) = ax+ b
f(x+1) = a(x + 1) + b = ax + a + b = ax+b + a = f(x) + a
Calcul du coefficient directeur.
Parfois nous n’avons pas l’équation de la droite, mais nous connaissons des points par laquelle elle passe.
Juste deux points nous permettent de retrouver l’équation de la droite !
Si vous savez que Laura a regardé un film supplémentaire et a payé 40€, alors que Roger a regardé 4 films supplémentaire et a payé 55€,
Comment retrouver le coefficient directeur ?
Le coefficient donne le coût d’un film supplémentaire.
Ici, il suffit de regarder la différence entre ce qu’a payé Laura et Roger. Roger a payé 15€ en plus que Laura et il a regardé 3 films en plus par rapport à elle.
15€ pour 3 films : 15/3 = 5
Un film coûte 5€
Le coefficient directeur est 5.
👉🏻 De manière générale, si on connaît deux points de la droite A et B, voici la formule du coefficient directeur :
C’est exactement ce que nous avons fait avec Laura et Roger.
La différence des ordonnées, du prix payé ce mois-ci : 55 - 40 = 15
La différence des abscisses, du nombres de films supplémentaires vus : 4 - 1 = 3
Régression linéaire
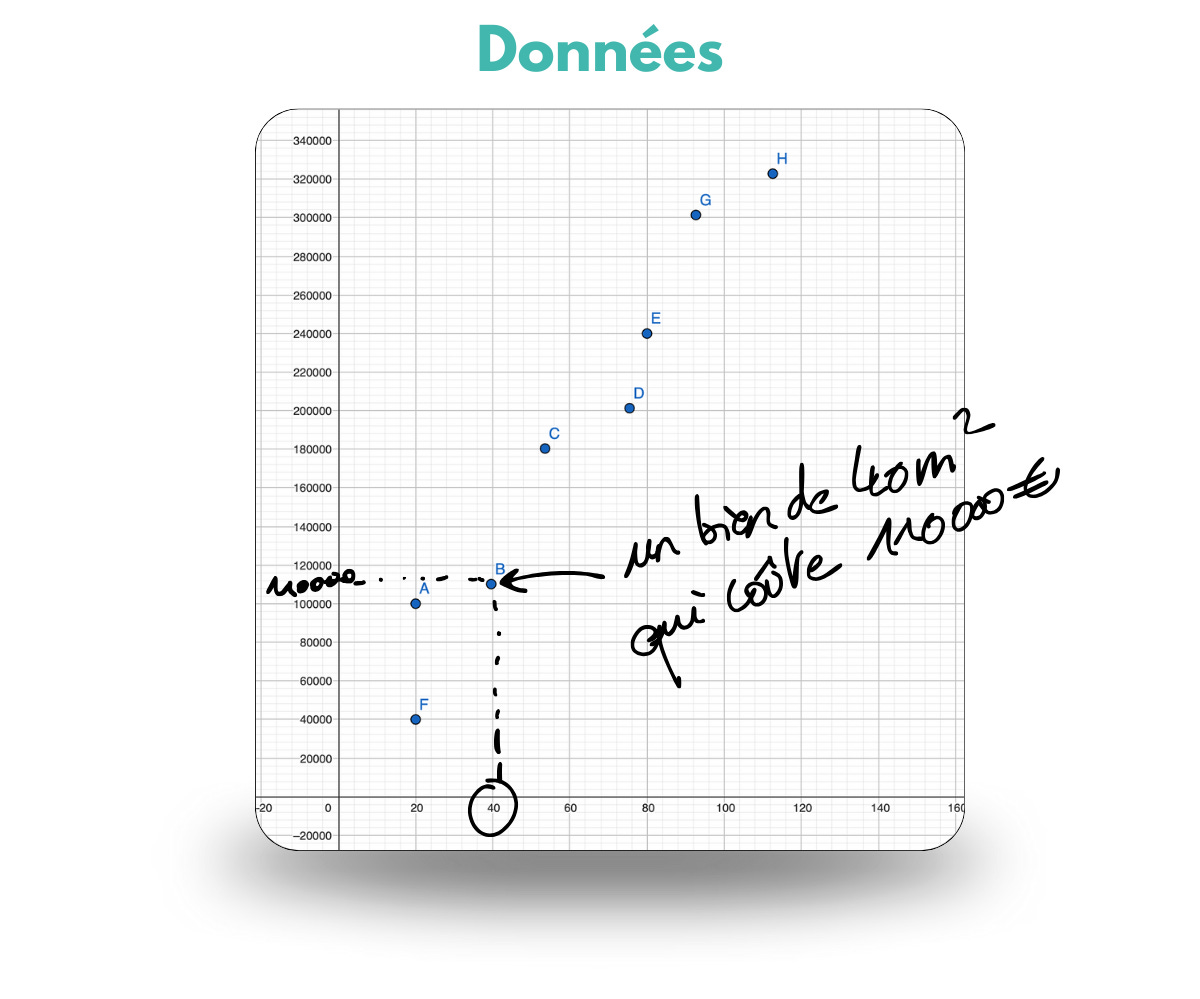
Prenons un exemple : le coût immobilier en fonction du mettre carré.
On a des données (le prix et la surface de biens immobiliers).
On veut trouver une fonction qui permette de retrouver le prix en fonction de la surface. Ou en tout cas, une fonction qui nous donne un résultat le plus proche possible de la réalité.
On cherche à modéliser nos données.
Un outil classique en data, est la régression linéaire.
On cherche une droite qui va modéliser nos données (les points sur le graphique).
Attention, un tel model est intéressant quand nos données ont l’air d’être proche d’une même ligne (on parle de linéarité).
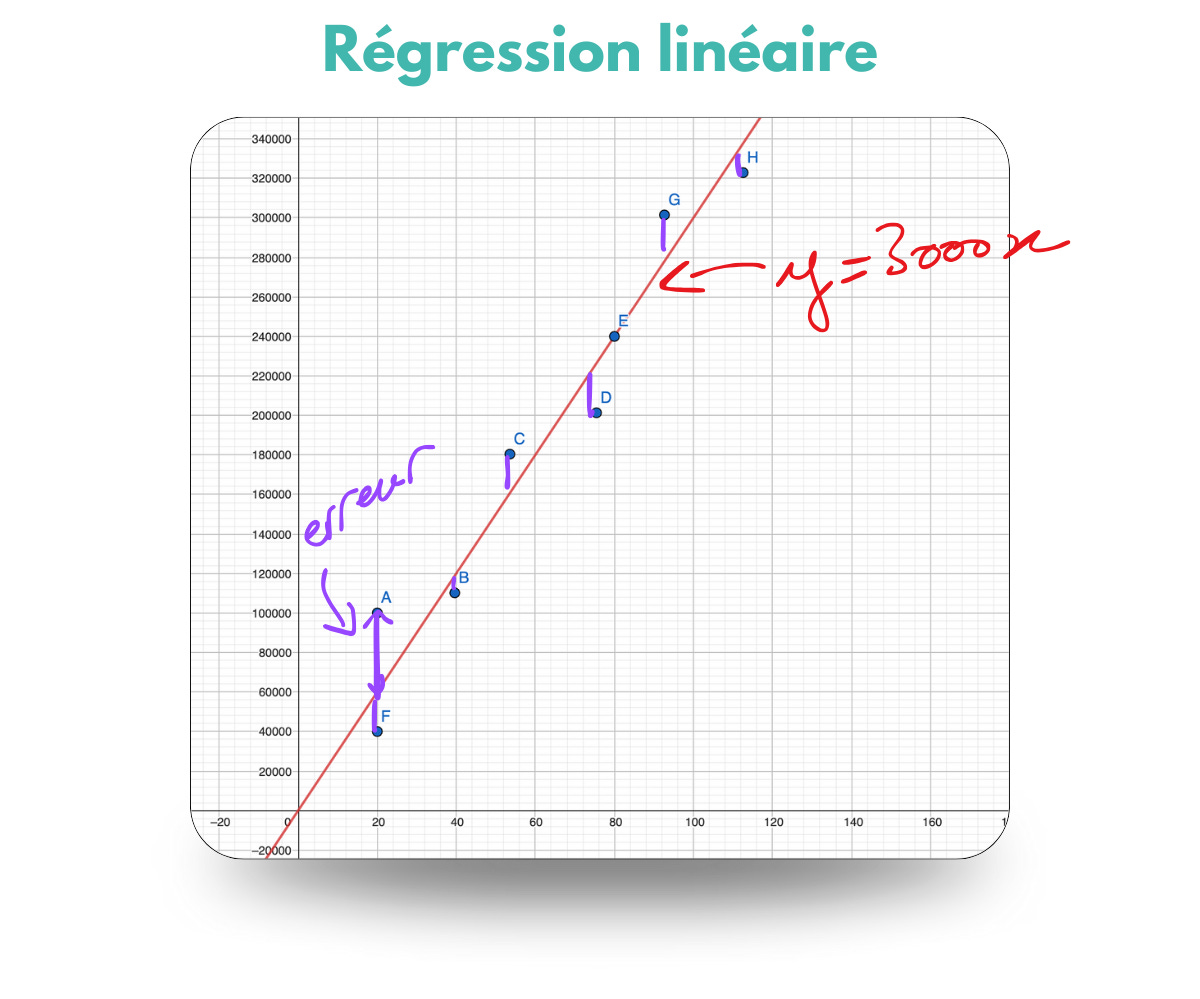
Dans ce cas, la régression linéaire va nous donner la droite la plus proche de nos points. Ou plus précisément, celle qui fera le moins d’erreur.
Pour se faire, on calcule les erreurs entre ce que la droite nous dit et la réalité (les points).
On crée une fonction qui mesure ces erreurs (souvent appelée fonction de coût ou de perte) et on cherche à la minimiser. Il y a plusieurs manières de faire. L’une d’elles est d’utiliser les dérivées (mais ce n’est pas le sujets de cette newsletter, je vous en parlerai une autre fois). 😉
Une fois la régression linéaire faite, on obtient cette droite qui modélise nos données.
Maintenant, on peut prédire quel sera la coût d’un bien immobilier à partir de sa surface.
Par exemple, un bien avec une surface de 100 m2 devrait coûter 3000 x 100 soit 300 000 euros.
💁🏻♀️ Voilà, maintenant vous en savez un peu plus sur la régression linéaire grâce à la fonction affine.
☝🏻 Avant de nous quitter je vous laisse cet exercice :
Quel est le coefficient directeur de la droite passant par les points E et K de coordonnées respectives ( - 7 ; 0 ) et ( 3 ; 5 ) ?
Vous sentez que vous avez besoin de revoir toutes ces notions et plus, pour votre reconversion en data ? Vous pouvez encore rejoindre mon programme :
Parcours Maths.
À bientôt 👋🏻







Je suis en plein algèbre linéaire et ça me parle beaucoup :)
Merci !
La réponse est "rise / run" soit (y1-y0)/(x1-x0) -> (5-0)/(3-(-7)) -> 5/10 -> 0.5 :p