Formule de Bayes…
#13 … ou comment renverser les conditions !
Bonjour à tous 👋🏻
Après avoir vu les probabilités conditionnelles dans la dernière édition, regardons de plus près une très belle et bien utile formule :
La formule de Bayes 😍
Vous êtes malade !!! 🤒
🪴 Plantons le décor :
Vous pensez être atteint de la maladie M.
1 personne sur 100 000 a cette maladie.
Paniqué, vous allez voir Dr Maboul.
🧑🏻⚕️ Dr. Maboul vous fait passer un test médical, il est positif. (Aïe !)
Il vous dit :
“ Lors de l’étude, sur 100 malades, le test a été positif pour 99 d’entre eux. Et le test se trompe pour seulement 1 personne sur 100 personnes qui ne sont pas malades.
Votre test étant positif, il y a 99% de chance que vous soyez malade !
C’est la Science qui le dit ! Les chiffres ne mentent pas ! ”
Devez-vous le croire ?
En d’autres termes, Dr Maboul vous dit que la probabilité que vous soyez malade sachant que le test est positif est de 0,99
Revoilà nos probabilités conditionnelles !
En fait, Dr Maboul vous raconte n’importe quoi !
Est-ce que c’est volontaire ? Est-ce qu’il n’a pas bien suivi ses cours de probabilités ? Ça, nous ne le saurons jamais et ce n’est pas le sujet. 🤷🏻♀️
🔎 Passons à la loupe ce qu’il vous a dit.
Arbre de probabilité 🌳
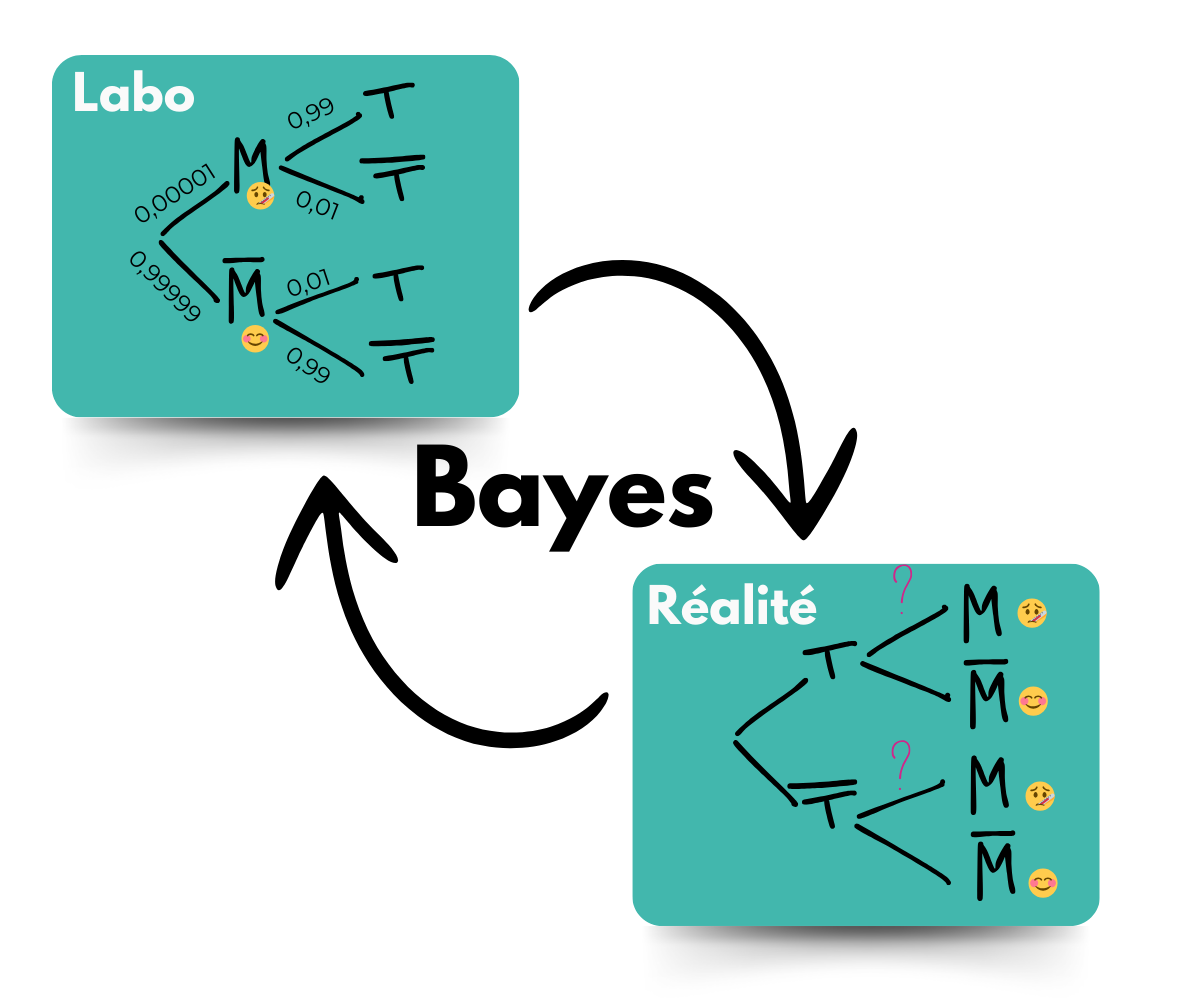
Nous pouvons construire un arbre de probabilité à partir des infos reçues.
1️⃣ “ Lors de l’étude, sur 100 malades, le test a été positif pour 99 d’entre eux. “
Cette phrase signifie que si on prend un malade, il a 99% de chance que son test soit positif. Mais dans ce cas, on sait déjà que la personne est malade.
On a donc P(T|M) = 0,99
C’est la probabilité d’avoir un test positif sachant qu’on est malade.
(Ce qui n’est pas pareil que la probabilité d’être malade sachant que le test est positif.)
2️⃣ ”Et le test se trompe pour seulement 1 personne sur 100 personnes qui ne sont pas malades.”
Autrement dit, quand on sait que la personne n’est pas malade, il y a une chance sur 100 pour que le test soit quand même positif. On a donc P(T| non M) = 0,01
3️⃣ Nous savons que : 1 personne sur 100 000 a cette maladie.
La probabilité d’être malade est donc de 1/100 000. On peut en déduire la probabilité de ne pas être malade : 1 - 1/100 000 = 99 999/ 100 000
Maintenant, on peut remplir notre arbre de probabilités.
Bayes à la rescousse !
Là, on a un arbre de probabilité de ce qui se passe au labo, pendant les essais, mais pas dans la réalité.
Car dans la réalité, tout le problème est de savoir si l’on est malade ou non. Ce que l’on peut savoir, c’est si notre test est positif ou négatif. Et c’est tout.
Voilà l’arbre qui nous intéresse 👇🏻
Et, TADAM, heureusement, le théorème de Bayes arrive à la rescousse 🦸🏻
Il est beau, il est fort, il est masqué et il a un super pouvoir : inverser les conditions.
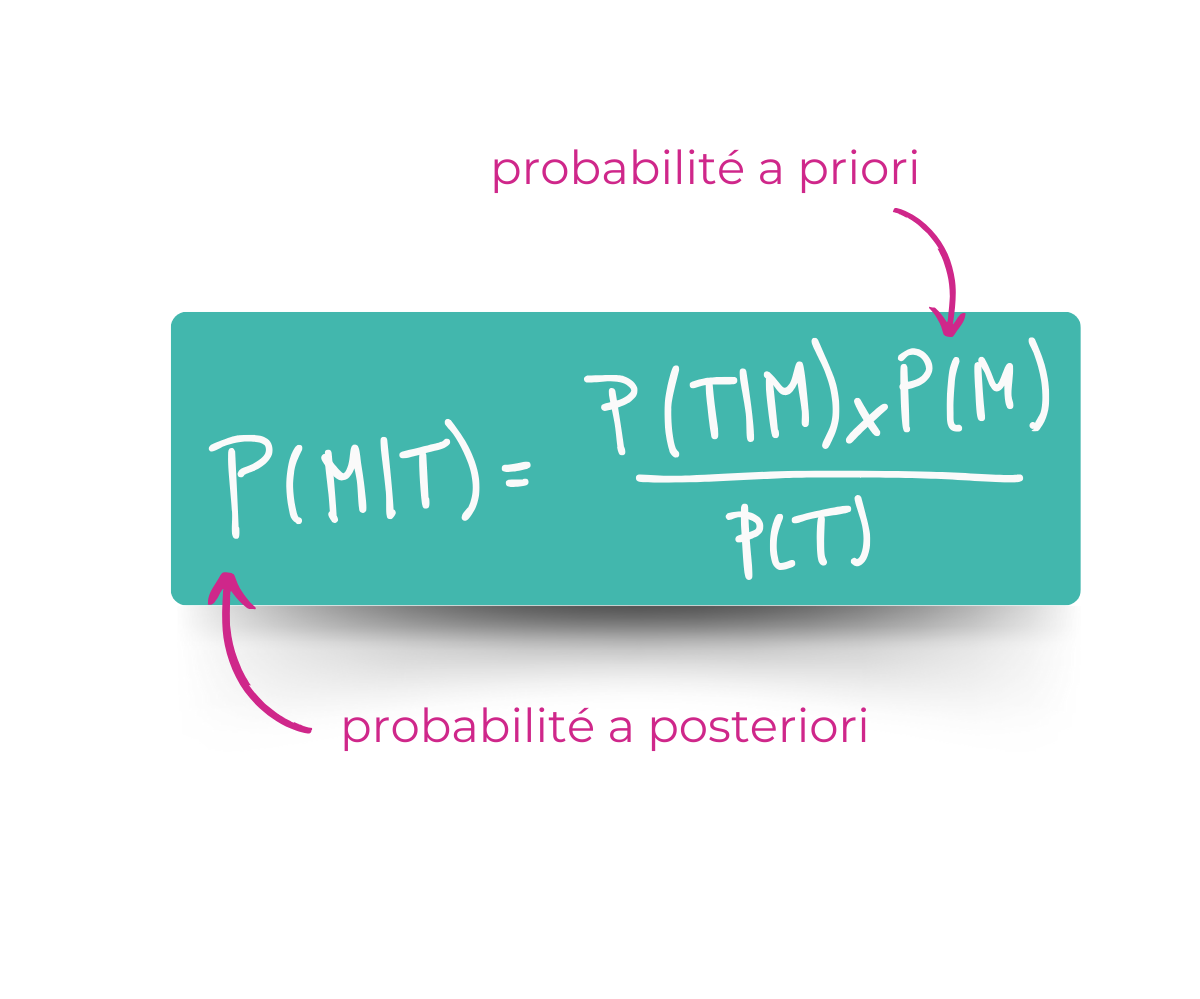
Il nous dit que :
On retrouve la formule ainsi :
Grâce aux données obtenues au labo, on connaît P(T|M) et P(M).
Par contre, on ne connait pas P(T) .
Mais pas de soucis ! On peut le retrouver grâce au premier arbre de probabilités.
Conclusion :
Après que votre test soit positif, vous avez 0,1% de chance d’être malade.
On est bien loin des 99% 😱
C’est quoi le problème ?
Voyez-vous ce qui donne cette si grande différence entre la “performance” du test dans le labo et dans la réalité ?
Au labo, on a pris 100 personnes malades et 100 personnes non malades. Mais dans la réalité, il n’y a qu’une personne malade sur 100 000.
Prenons 1 personne malade et 99 999 personnes non malades.
Disons que la personne malade a bien un test positif.
Sur les 99 999 non malades, à cause de l’erreur de 1 sur 100 du test, il y aura presque 1000 personnes non malades avec un test positif.
On a donc 1001 personnes avec un test positif.
1 est malade + 1000 ne sont pas malades.
Vous faites partie de ces personnes avec un test positif. Soit vous êtes cette seule personne malade, soit vous êtes dans les 1000 personnes qui ne sont pas malades.
Vous avec donc beaucoup plus de chance de ne pas être malade !
La morale de l’histoire !
Pour bien comprendre les chiffres que l’on nous donne, il faut un minimum de connaissances en probabilités, en statistiques etc…
Même sans vouloir induire en erreur, on peut, sans s’en rendre compte, mal interpréter des données. 😕
Si vous vous orientez vers la data analyse ou data science, les maths sont juste incontournables !!
Je termine avec une petite info sur Parcours Maths,
mon programme de remise à niveau,
→ Je fais -30% pour les étudiants ou demandeurs d’emploi 😉
Il suffit de me le demander par mail ( annelise@maprofdemaths.com) avant de faire l’achat !
Probabilités a priori et a posteriori
Mais avant de se quitter, je vous explique deux notions que vous avez peut-être déjà croisées :
La probabilité a priori et la probabilité a posteriori.
👉🏻 La probabilité a priori se base sur la généralité et non sur l’expérience (l’expérience, ici, c’est le test). Donc avant l’expérience.
👉🏻 La probabilité a posteriori se base sur les données de l’expérience (sur le résultat de votre test). Donc après l’expérience.
Sur ce, je vous souhaite une excellente semaine !
Et à bientôt pour encore plus de maths. 👋🏻