Hello 👋🏻
C’est parti pour la 2ème édition de “La Pause Maths”. On continue de plonger en douceur dans les maths. Aujourd’hui une lecture tranquille, pas de calcul. Mais ne vous méprenez pas, les calculs vont arriver. 😇
Ces lettres qui viennent nous bousculer.
Pour certains, c’étaient les divisions, d’autres les fractions ou encore les pourcentages. Tout le monde, à un moment donné, s’est senti un peu largué devant tous ces chiffres.
Puis un jour, sans que l’on s’y attende, le prof commence à mettre des lettres dans les calculs. Et là, BOOM, 🤯 :
“Que viennent faire ces purées de lettres parmi les chiffres ?”
(oui, moi, je dis “purée” 😇)
C’est une phase assez déroutante dans l’apprentissage des maths. Pourtant, l’arrivée des lettres, c’est-à-dire, le calcul littéral, est une grande avancée !
Mais cette grande avancée nous paraît plutôt être un énième plan foireux que nous propose notre prof de maths.
J’ai vu des élèves se mélanger complètement les pinceaux avec le calcul littéral.
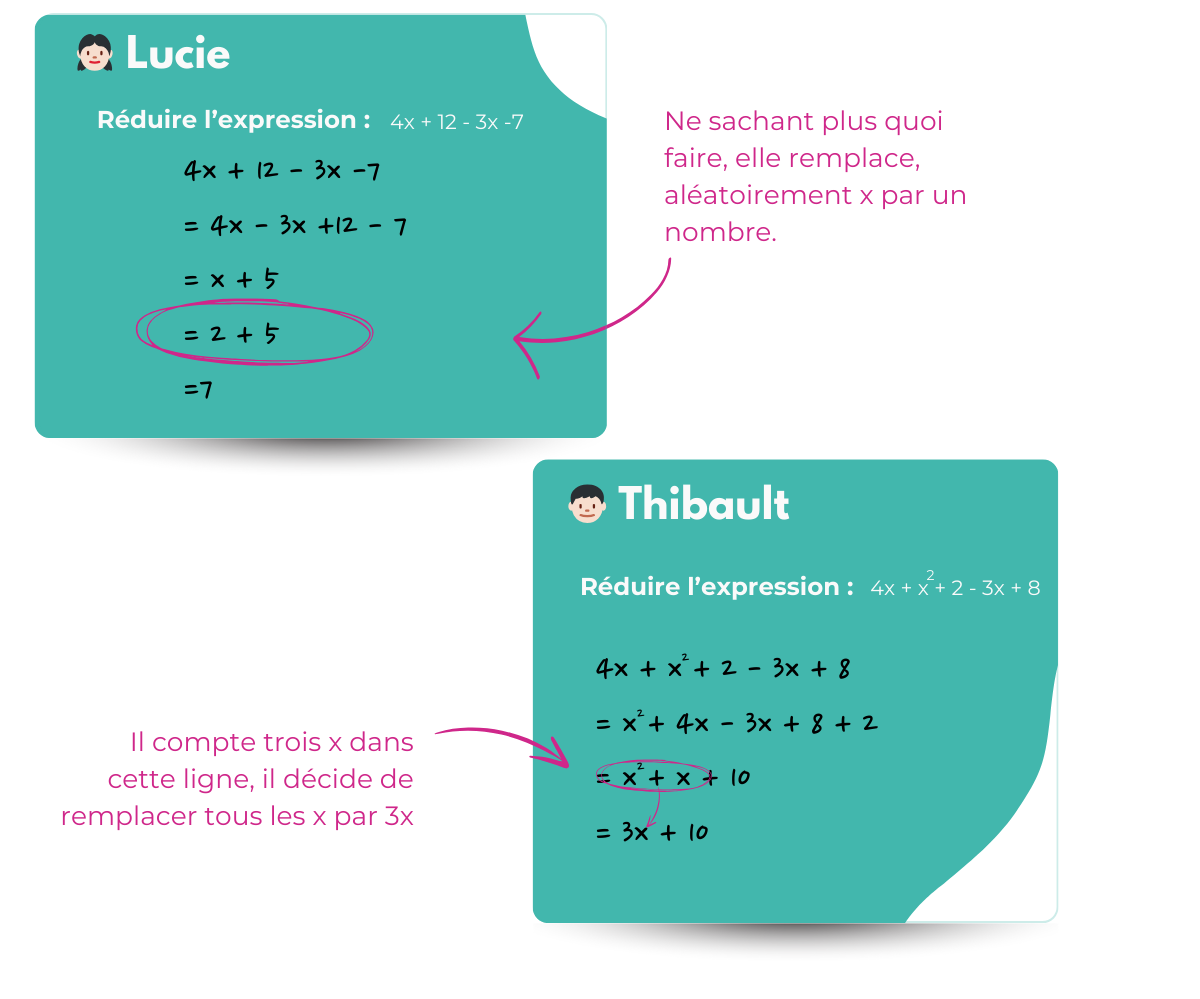
👧🏻 Coincée devant x + 5, Lucie continue son calcul par 2 + 5 = 7
Elle était soulagée d’avoir pu finir le calcul !
Lui demandant pourquoi elle a remplacé x par 2, elle me répond : “Je ne savais pas quoi faire, alors j’ai tenté”.
👦🏻 Thibault devant x + x^2 + 10, écrit “ = 3x + 10”
Je vois ce qu’il a voulu faire : x + x^2 + 10 = x + x fois x + 10
Ça il le sait. Et comme il a compté trois x dans x + x^2, alors il a décidé de remplacer tout ce beau monde par 3x, tout simplement !
Le calcul littéral peut nous laisser perplexes. On ne voit pas comment finir le calcul et on ne veut pas clôturer sur un x + 10 ou encore sur un x + x^2 + 10.
Cela nous laisse un sentiment d’inachevé et de mystère : “mais qui se cache derrière ce purée de x ?”
Les élèves tentent des choses, espérant que la magie mathématique opère.
Et c’est là leur erreur ! Il n’y a rien de magique en maths.
Les maths sont belles et fascinantes mais pas magiques !
Quand on ne comprend pas ce que fait le prof, on y voit un tour de passe-passe. 🪄
On accepte que ce tour de passe-passe ne soit pas à notre portée. Alors, à notre manière, on tente un tour. Et souvent, ça ne marche pas.
☝🏻 La difficulté du calcul littéral est pourtant sa puissance : c’est l’une des premières rencontres mathématiques qui nous pousse dans l’abstraction.
En primaire, pour apprendre les soustractions, on nous dit : Julie a 4 stylos, Tom lui en prend 3, combien lui en reste-t-il ?
Mais dans le calcul littéral : plus besoin de Tom, de Julie et de ses stylos multicolores. 4x - 3x peut se calculer, seul, dans le monde de l’abstraction, sans savoir ce que x représente.
Voilà la puissance du calcul littéral. On peut créer des formules abstraites qui s’appliqueront à plein de cas réels.
Alors d’où vient cette idée de génie ?
Les symboles mathématiques +, -, x nous sont si familiers qu’on pourrait oublier qu’ils n’ont pas toujours existé. Réfléchissez un instant à devoir noter des formules mathématiques sans symbole, mais avec des phrases. C’est ce qu’ont fait pendant longtemps les mathématiciens. Autant vous dire qu’il fallait s’accrocher pour lire un bouquin de maths. 😱
Les équations vous paraissaient peut-être difficiles au collège, mais imaginez devoir résoudre ça :
“Je prends trois fois un poids inconnu de biscuits dans mon sac, j’y ajoute un même poids de brioche, j’ajoute deux petits sacs dans lesquels se trouve ce poids en bonbons ainsi qu’une guimauve pesant quatre grammes. Mon gros sac pèse cent-cinquante grammes. Que vaut le poids inconnu ?”
Heureusement, dès le XVe siècle des signes comme + et - font leur apparition. Nous voilà soulagés de pouvoir écrire de manière plus succincte les formules mathématiques.
👉🏻 En 1591, le français, François Viète, publie un ouvrage mathématique dans lequel il propose d’utiliser :
les voyelles pour nommer les nombres inconnus des équations
les consonnes pour les nombres connus.
Grâce à François Viète, la phrase énoncée plus haut, peut se résumer par :
3x + 2x + 2(x+4) = 150
Enfin, non, François aurait écrit : 3a +2a + 2(a+4) = 150
L’utilisation de notre bon vieux x, nous vient de Descartes !
En effet, c’est René Descartes qui proposera d’utiliser les premières lettres de l’alphabet pour les nombres connus et les dernières lettres de l’alphabet pour les nombres inconnus. Et c’est ce que nous faisons aujourd’hui !
Nouveau calcul, nouvelles méthodes
Regardons cette équation :
3x +2x + 2(x+4) = 150
3x+2x ça fait 5x : pas besoin de savoir ce qui se cache derrière ce x.
L’important, c’est qu’il se cache la même chose derrière tous les x.
Nous pouvons donc les regrouper.
L’élève arrivant devant, 2(x+4), se retrouve une nouvelle fois embêté. 😓
Il sait que les parenthèses sont prioritaires, mais il ne peut rien faire de x + 4.
Avec le calcul littéral, nous apprenons, entre autre, deux nouvelles méthodes de calculs pour nous sortir de ce pétrin :
Le développement et la factorisation.
Mais on va s’arrêter là pour aujourd’hui. La prochaine fois, nous commencerons à mettre les pieds dans le petit bain des calculs. 😉
En attendant, on se retrouve sur LinkedIn
À bientôt ! 👋🏻
👉🏻 Petit instant pub :
Si vous avez besoin de replonger dans les maths avec des cours, mon programme de révision en autonomie “Parcours Maths” est à 200€ au lieu de 280€ jusqu’au 14/07/2024 avec le code SUN80 !
Pour en savoir plus, c’est par ici : https://maprofdemaths.systeme.io/parcours_maths_data
La pub est finie 😇