À l'abordage des structures algébriques...

#9 ... avant de plonger dans l'algèbre linéaire.

Bonjour tout le monde ! 👋🏻

Si vous êtes en reconversion dans la data science, vous allez être confronté à de l’algèbre linéaire. Mais avant d’aller par là-bas, il vous faut faire une petite pause dans ce qu’on appelle les structures algébriques.

Et c’est ce que nous allons faire dans cette 9ème édition.

On y va ! 🙂

---

Des cas particuliers.

Le monde des mathématiques est bien plus vaste que ce que l’on nous montre au collège ou au lycée. Les notions que nous y apprenons ne sont souvent que des cas particuliers d’idées beaucoup plus générales.

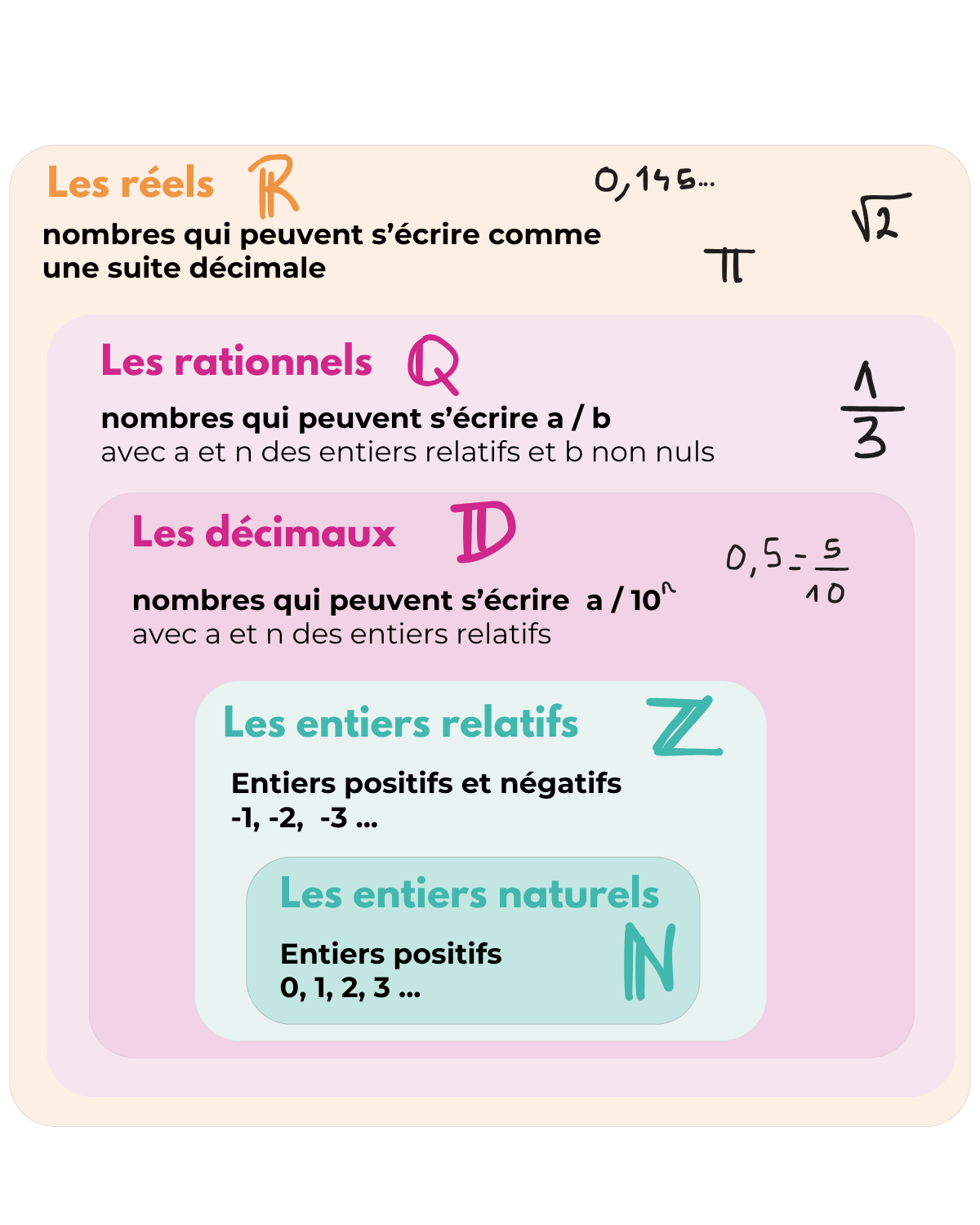
Vous connaissez peut-être déjà les ensembles de nombres.
Voici de quoi vous rafraîchir la mémoire.👇🏻

Un ensemble en maths, ce n’est pas forcément un ensemble de nombres.

On peut avoir un ensemble de matrices, un ensemble de vecteurs, un ensemble de fonctions. Bref, un ensemble d’éléments mathématiques.

👉🏻 Prenons un ensemble (les entiers naturels), on va le munir d’une opération : l’addition. L’ensemble N avec l’addition + est une structure (N,+).
On se demande quelles particularités a cette structure. Et selon ses particularités, on pourra dire plus précisément de quelle structure il s’agit.

Pour ça, on a besoin de vocabulaire.

Vocabulaire.

👉🏻 Commençons par l’élément neutre. Vous en connaissez déjà 😉 sauf qu’on ne le présente pas ainsi à l’école.

L’élément neutre d’un ensemble par rapport à une opération, est l’élément qui ne va rien changer !
Pour l’addition, c’est l’élément e tel que
a + e = e + a = a

Vous l’avez trouvé ?

C’est 0.

Et oui : a + 0 = a

Par exemple : 3 + 0 = 3

Si nous prenions la multiplication comme opération, quel serait l’élément neutre ?
( a x e = e x a = a )

C’est 1.

a x 1 = a

par exemple : 6 x 1 = 6

🔎 Regardons dans notre ensemble des entiers naturels muni de l’addition.
Il y-a-t-il un élément neutre ? Oui, 0 est bien dans l’ensemble des entiers naturels.

👉🏻À partir de l’élément neutre nous pouvons définir ce qu’est un symétrique.

y est symétrique de x par rapport à l’opération *, si et seulement si
x * y = y * x = e (l’élément neutre)

Dans notre cas y est symétrique de x si et seulement si
x + y = y + x = 0
Qui est y ?

y = -x

En effet : x + (-x) = 0

Donc ici, le symétrique de 2 est (-2).
2 + (-2) = 0

Le symétrique de (-7) est 7
(-7) + 7 = 0

Dans ce cas de l’addition, on appelle ce symétrique un opposé. C’est le terme que l’on apprend au collège.

🧠 Réfléchissez maintenant :
Quel est le symétrique de a par rapport à la multiplication ?

C’est 1/a.

a x (1/a) = 1 (1 est l’élément neutre pour la multiplication)
Le symétrique de 4 est 1/4.

Dans ce cas de la multiplication, on appelle ce symétrique un inverse. C’est aussi ce que l’on apprend au collège.

🔎 Retournons à notre ensemble des entiers naturels muni de l’addition.
Contient-il tous les symétriques de ses éléments ?

Non…

Le symétrique de 2 est (-2) mais (-2) n’est pas un entier naturel.

Par contre, si on prend l’ensemble des entiers relatifs Z (donc avec les entiers négatifs) muni de l’addition, cet ensemble contient bien tous les symétriques de ses éléments.

Maintenant, nous allons nous pencher sur certaines propriétés que peuvent avoir les opérations.

Propriétés

👉🏻 L’associativité
C’est une propriété que l’on utilise, mais en général, on ne sait juste pas qu’elle s’appelle ainsi.

Prenons 3 éléments d’un ensemble : a, b et c.
L’opération * est associative si et seulement si :
(a*b)*c = a*(b*c)
On s’en fiche de l’ordre dans lequel on fait l’opération !

Avec nos entiers et l’addition cela donne :
(a+b)+c = a+(b+c)

🔎 Et c’est effectivement le cas. L’addition est associative avec les entiers naturels. exemple :
(2+3)+7 = 5 + 7 = 12
2 + (3+7) = 2 + 10 = 12

👉🏻 La commutativité

Vous la connaissez aussi. Elle nous dit que l’on peut inverser les places des éléments d’une opération et le résultat sera le même.
a + b = b + a

🔎 L’addition est bien commutative pour l’ensemble des entiers naturels.

Exemple : 2 + 3 = 3 + 2 = 5

💡 Remarque : si vous avez déjà vu les matrices, vous savez que la multiplication n’est pas commutative pour les matrices.
AB peut être différent de BA.

Les propriétés évidentes pour les nombres ne sont pas forcément applicables à d’autres objets mathématiques.

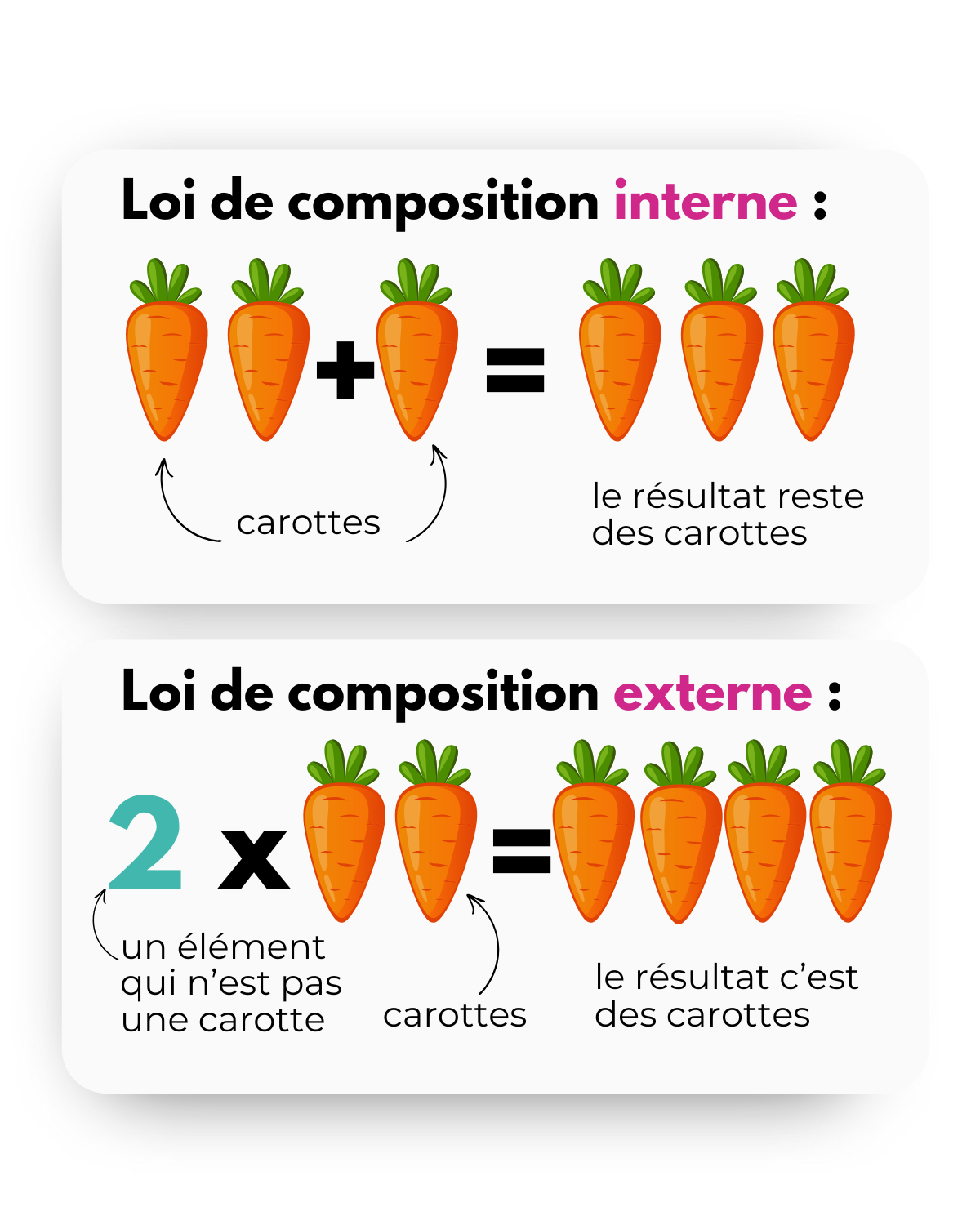
Loi de composition interne et externe

Les opérations dont je vous parle depuis le début, on les appelle aussi des lois de composition. Elles peuvent être internes ou encore externes.

👉🏻 Une loi est interne quand elle prend deux éléments d’un ensemble et que le résultat est aussi dans l’ensemble. C’est le cas pour les entiers naturels et l’addition.

Si on prend deux entiers naturels a et b, a + b est aussi un entiers naturels (par exemple 5 + 9 = 14 est un entier naturel).

👉🏻 Une loi est dite externe quand elle prend un élément d’un ensemble F et un autre dans E (ensemble différent de F) et que le résultat est dans E.

Exemple :
Soit f une fonction. Si on multiplie f par 2, on obtient une fonction ( g(x) = 2f(x) )

À l’attaque du groupe.

Nous avons maintenant assez de vocabulaire pour comprendre ce qu’est un groupe
(G, *).

C’est un ensemble G (non vide) muni d’une loi interne *, tel que :

• la loi * est associative

• Il existe un élément neutre

• tout élément de G a un symétrique

Si en plus la loi * est commutative on parle d’un groupe commutatif (ou d’un groupe abélien).

À vous : (N,+) est-il un groupe ?

+ est bien une loi de composition interne et elle est associative. ✅
0 est l’élément neutre et appartient bien à N. ✅
Par contre il n’y a pas de symétrique dans N. ❌

Ce n’est donc pas un groupe.

Par contre (Z,+) est un groupe ! Et même un groupe commutatif.

Et (Z, . ) ? Est-ce un groupe ? ( “.” est la multiplication)
Dîtes-moi pourquoi en commentaire !

Autres structures

Regardons rapidement deux autres structures et on s’arrêtera là ! 😇

👉🏻 Un anneau (A , + , . ) est une extension d'un groupe.
Il a deux opérations, généralement appelées addition et multiplication (ici, je l’ai notée “.” j’aurai pu la noter “x” ), avec les propriétés suivantes :

• (A, +) est groupe commutatif
  (commutativité : a + b = b + a)

• La multiplication est une loi de composition interne.

• Elle est associative :
  a . (b . c) = (a . b) . c .

• Distributivité de la multiplication sur l’addition :
  a . (b + c) = a.b + a.c.

• La multiplication admet un élément neutre.

(Mais, il n'y a pas nécessairement d'inverse multiplicatif pour tous les éléments !)

Exemple : Les entiers relatifs avec l'addition et la multiplication forment un anneau. L’élément neutre de la multiplication est 1.
(ex : 2 x 1 = 2)

👉🏻 Un corps (K , + , x) est un anneau avec une propriété supplémentaire 👇🏻

Tous les éléments (autres que l’élément neutre par rapport à l’addition, donc les éléments non nuls) ont un symétrique par rapport à la multiplication.
(ex : 4 x 1/4 = 1)
En fait, (K*, x) est un groupe.
(K* signifie que l’on prend K sans 0)

Exemple : les entiers avec l'addition et la multiplication (Z, +, x) forment un anneau mais pas un corps car tous les éléments n’ont pas forcément de symétrique par rapport à la multiplication (le symétrique de 5 serait 1/5 car 5x1/5 = 1 mais 1/5 n’est pas un entier).

Les maths ça peut paraître compliqué notamment parce qu’il y a beaucoup de vocabulaire, mais on a besoin de cette base en vocabulaire pour comprendre la suite.

Alors bravo d’avoir lu entièrement cette newsletter, vous avez maintenant plus de vocabulaire pour la suite de votre apprentissage en maths !

D’ailleurs, est-ce que des cours vidéo sur les bases de l’algèbre linéaire jusqu’à la compréhension de l’A.C.P. avec des exercices, vous intéresseraient ?
Si c’est le cas, inscrivez-vous via le lien : https://maprofdemaths.systeme.io/algebre_lineaire

Je suis déjà en train de bosser dessus.
Et vous serez parmi les premiers à être informés de sa sortie ! 😎

En attendant, on se retrouve sur LinkedIn !

À bientôt 👋🏻